Question

Given that the length of a rectangle is 14 cm and one of its diagonal is 17 cm. Find its area.

Answer 1

Hint: Rectangle is a quadrilateral whose opposite sides are equal.
The angle between two adjacent sides of the rectangle is ${90^ \circ }$.
Here we solve by looking at the right angled triangle \[\vartriangle ABC\] whose two sides are given, therefore using Pythagoras theorem we find the length of perpendicular side (which is also the breadth of the rectangle) and finally substitute the values to find the area of rectangle
Pythagoras theorem can be applied to every right angle triangle.
Pythagoras theorem: square of the hypotenuse is equal to the sum of the square of base and square of perpendicular.
In a right angled triangle, base and perpendicular are at the angle of $90^\circ $ to each other and hypotenuse is the longest side.

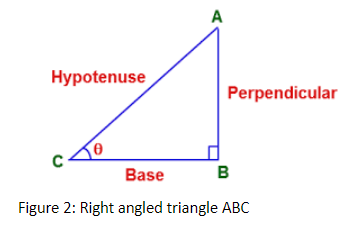
$\mathop {{\text{Hypotenuse}}}\nolimits^{\text{2}} {\text{ = }}\mathop {{\text{ Base}}}\nolimits^{{\text{2 }}} {\text{ + }}\mathop {{\text{ Perpendicular}}}\nolimits^{\text{2}} $

Complete step by step solution:
Step 1:

Step 2
Length AB = 14 cm ($\because $given)
Step 3
Length AB = length CD = 14 cm ( $\because $opposite sides of rectangle)
                                                                                                                                                        …… (1)
Step 4
Diagonal AC = 17 cm (\[\because \]given)
                                                                                                                                                        …… (2)
Step 5
Length AB and breadth BC are perpendicular. ($\because $property of rectangle)
Step 6
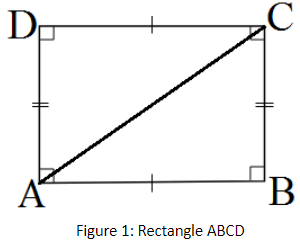
Length AB, breadth BC and diagonal AC forms a right-angled triangle $\vartriangle $ABC, right angled at vertex B of rectangle ABCD in figure 1.
Using Pythagoras theorem on $\vartriangle $ABC
    $\mathop {{\text{Hypotenuse}}}\nolimits^{\text{2}} {\text{ = }}\mathop {{\text{ Base}}}\nolimits^{{\text{2 }}} {\text{ + }}\mathop {{\text{ Perpendicular}}}\nolimits^{\text{2}} $
      $\mathop {{\text{AB}}}\nolimits^2 + \mathop {{\text{BC}}}\nolimits^{\text{2}} {\text{ }} = {\text{ }}\mathop {{\text{AC}}}\nolimits^{\text{2}} $
  $\mathop { \Rightarrow {\text{ 14}}}\nolimits^{\text{2}} + \mathop {{\text{BC}}}\nolimits^{\text{2}} {\text{ }} = {\text{ }}\mathop {17}\nolimits^2 $ (from (1) and (2))
  $ \Rightarrow {\text{ }}196 + \mathop {{\text{BC}}}\nolimits^2 {\text{ = }}289$
  $ \Rightarrow \mathop {{\text{ BC}}}\nolimits^{\text{2}} = 289 - 196 = 93$
                     \[{\text{BC}} = \sqrt {93} \]cm …… (3)
Step 7
Area of rectangle = length $ \times $breadth
                                = AB $ \times $BC
                                $ = 14 \times \sqrt {93} $ (from (1) and (3))
                                $ = 14\sqrt {93} $$\mathop {{\text{cm}}}\nolimits^2 $
Therefore, The area of the rectangle is $14\sqrt {93} $$\mathop {{\text{cm}}}\nolimits^2 $

Additional information: Perimeter of a rectangle is two times the sum of its length and breadth.
Perimeter of rectangle$ = 2({\text{length + breadth}}){\text{ }}units$

Note:
 The diagonal of the rectangle bisects its area.
The alternate method to find the area is:
Area of $\vartriangle $ABC $ = \dfrac{1}{2}{\text{base}} \times {\text{height}}$
                          = $\dfrac{1}{2} \times {\text{AB}} \times {\text{BC}}$= $\dfrac{1}{2} \times 14 \times \sqrt {93} $
                           =$7\sqrt {93} \mathop {{\text{cm}}}\nolimits^2 $
Area of $\vartriangle $ABC = Area of $\vartriangle $ADC = $7\sqrt {93} \mathop {{\text{cm}}}\nolimits^2 $
Area of rectangle ABCD = Area of $\vartriangle $ABC + Area of $\vartriangle $ADC
                                          $ = 7\sqrt {93} \mathop {{\text{cm}}}\nolimits^2 + \;7\sqrt {93} \mathop {{\text{cm}}}\nolimits^2 \;$
                                           $ = 14\sqrt {93} $$\mathop {{\text{cm}}}\nolimits^2 $