Question

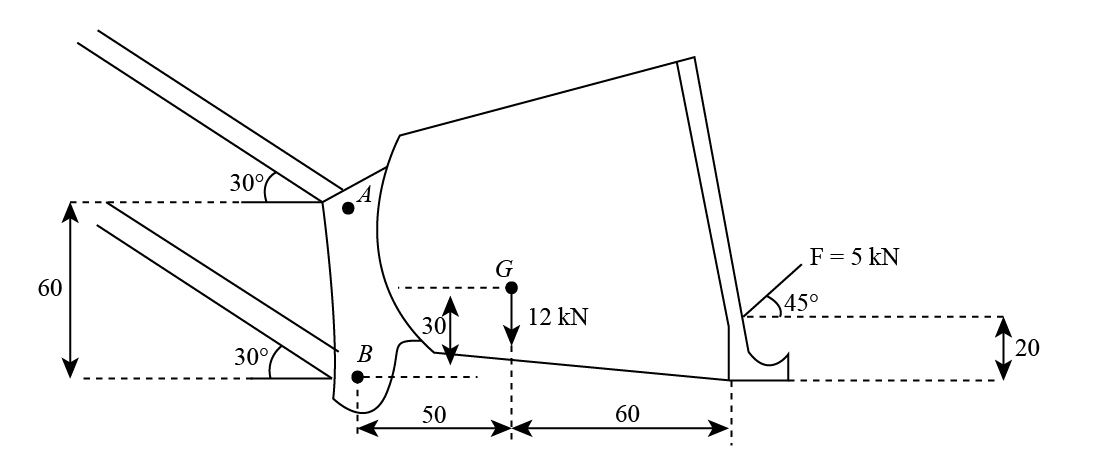
Given figure shows a shovel used to lift earth (sand). A and B are hinges connecting the shovel to the two rods shown. The weight of the shovel and sand is \[12\;{\rm{kN}}\] acting at G

A. \[0\;{\rm{kN}}\]
B. \[9.8\;{\rm{kN}}\]
C. \[17.66\;{\rm{kN}}\]
D. \[20\;{\rm{kN}}\]

Answer 1

Hint: The above problem can be resolved by taking the summation of moments of forces acting about point B. Along with this, the sum of horizontal as well as the vertical components of force is to be calculated to find the required result.


Complete step-by-step solution
Given:
The free body diagram for the given condition is shown as below showing the reaction forces at A and B, along with their respective x and y components.

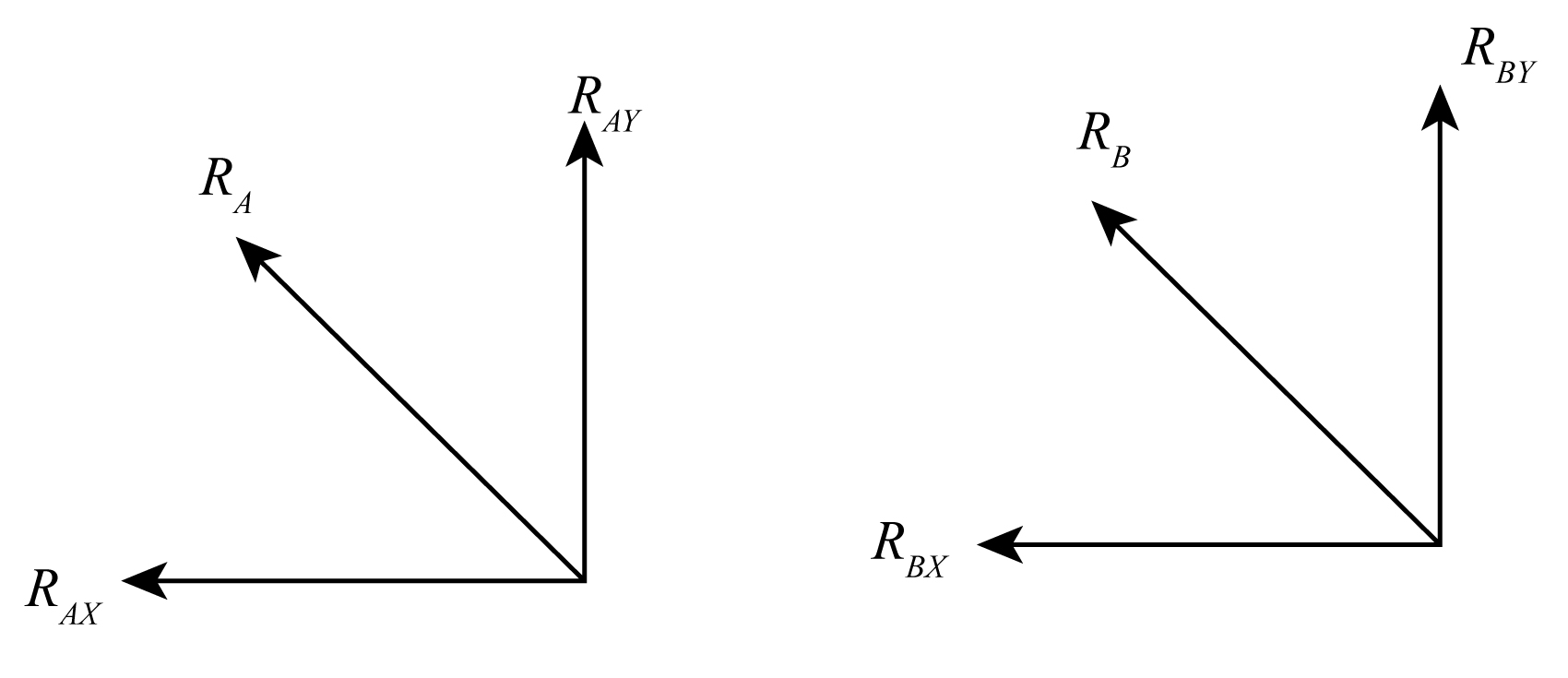
Here, \[{R_A}\] and \[{R_B}\] are the components of reaction force at point A and B.
From the given figure, applying the sum of moment about B as,
\[\begin{array}{l}
\sum {{M_B} = 0} \\
12\;{\rm{kN}} \times {\rm{50}} - \left( {5\cos 45^\circ } \right) \times {\rm{20}} + {\rm{ }}\left( {5\sin 45^\circ } \right) \times 110 - \left( {{R_A}\cos 30\;^\circ } \right) \times 60 = 0\\
{R_A} = 17.66\;{\rm{kN}}
\end{array}\]


 Taking sum of horizontal component of forces as,
\[\begin{array}{l}
\sum {{F_x} = 0} \\
 - {R_{Bx}} - {R_A}\cos 30\;^\circ - 5\cos 45\;^\circ = 0\\
 - {R_{Bx}} - \left( {17.66\;{\rm{kN}}} \right) \times \cos 30\;^\circ - 5\cos 45\;^\circ = 0\\
{R_{Bx}} = - 18.83\;{\rm{kN}}
\end{array}\]
 Taking sum of vertical component of forces as,
\[\begin{array}{l}
\sum {{F_y} = 0} \\
{R_{By}} + {R_A}\sin 30\;^\circ - 12\;{\rm{kN}} - 5\sin 45\;^\circ = 0\\
{R_{By}} + \left( {17.66\;{\rm{kN}}} \right) \times \sin 30\;^\circ - 12\;{\rm{kN}} - 5\sin 45\;^\circ = 0\\
{R_{By}} = 6.705\;{\rm{kN}}
\end{array}\]
The reactive force at B is,
\[\begin{array}{l}
{R_B} = \sqrt {R_{Bx}^2 + R_{By}^2} \\
{R_B} = \sqrt {{{\left( { - 18.83\;{\rm{kN}}} \right)}^2} + {{\left( {6.705\;{\rm{kN}}} \right)}^2}} \\
{R_B} = 20\;{\rm{kN}}
\end{array}\]
Therefore, the magnitude of reactive force at B is \[20\;{\rm{kN}}\]and option D is correct.


Note: In order to resolve the given problem, one must be sure about the concepts of equilibrium of force at any specific points, along with the mathematical relations of moments of force and net force at any point. Moreover, the reaction force is to be properly mentioned by means of a correct free- body diagram, along with the direction of force. The sign conventions are properly taken into account to achieve the desired result.