Question

Given, \[D\] is the midpoint of side \[BC\] of a \[\vartriangle ABC\] . \[AD\] is bisected at the point \[E\] and \[BE\] produces cuts \[AC\] at the point \[X\] . Prove that \[BE:EX = 3:1\] .

Answer 1

Hint: To find the ratio \[BE:EX\] we will first construct \[DY\] parallel to \[BX\]. Then using the concept of similar triangles, we will prove the similarity of \[\vartriangle AEX\] and \[\vartriangle ADY\] and then similarity of \[\vartriangle BCX\] and \[\vartriangle DCY\]. Using the properties of similar triangles, we will find the ratio of different sides required and then using this we will find the ratio of \[BE:EX\].

Complete answer:

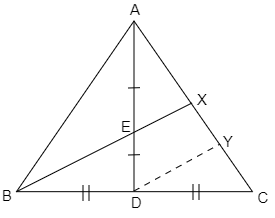
In \[\vartriangle AEX\] and \[\vartriangle ADY\], we have
\[\angle EAX = \angle DAY\] (Common)
\[\angle AXE = \angle AYD\] (By Corresponding angles)
Therefore, by angle-angle (\[AA\]) similarity
\[\vartriangle AEX \sim \vartriangle ADY\]
As when two triangles are similar, their corresponding sides are proportional.
From this we get in \[\vartriangle AEX\] and \[\vartriangle ADY\],
\[ \Rightarrow \dfrac{{EX}}{{DY}} = \dfrac{{AX}}{{AY}} = \dfrac{{AE}}{{AD}} - - - (1)\]
Since \[E\] is the midpoint of \[AD\], we can write
\[ \Rightarrow AE = ED\]
Now, as given
\[ \Rightarrow AD = AE + ED\]
Therefore, we can write
\[ \Rightarrow AD = AE + AE\]
On adding, we get
\[ \Rightarrow AD = 2AE\]
On rearranging,
\[ \Rightarrow \dfrac{{AE}}{{AD}} = \dfrac{1}{2} - - - (2)\]
Putting \[(2)\] in \[(1)\], we get
\[ \Rightarrow \dfrac{{EX}}{{DY}} = \dfrac{{AX}}{{AY}} = \dfrac{1}{2}\]
\[ \Rightarrow \dfrac{{EX}}{{DY}} = \dfrac{1}{2} - - - (3)\]
Now, in \[\vartriangle BCX\] and \[\vartriangle DCY\], we have
\[\angle BCX = \angle DCY\](Common)
\[\angle BXC = \angle DYC\] (By Corresponding angles)
Therefore, by angle-angle (\[AA\]) similarity
\[\vartriangle BCX \sim \vartriangle DCY\]
As when two triangles are similar, their corresponding sides are proportional.
From this we get in \[\vartriangle BCX\] and \[\vartriangle DCY\],
\[ \Rightarrow \dfrac{{BX}}{{DY}} = \dfrac{{CX}}{{CY}} = \dfrac{{BC}}{{DC}} - - - (4)\]
Since \[D\] is the midpoint of \[BC\]
\[ \Rightarrow BD = DC\]
Now, as given
\[ \Rightarrow BC = BD + DC\]
Therefore, we can write
\[ \Rightarrow BC = DC + DC\]
Adding right hand side, we get
\[ \Rightarrow BC = 2DC\]
On rearranging,
\[ \Rightarrow \dfrac{{BC}}{{DC}} = 2 - - - (5)\]
Putting \[(5)\] in \[(4)\], we get
\[ \Rightarrow \dfrac{{BX}}{{DY}} = \dfrac{{CX}}{{CY}} = 2\]
\[ \Rightarrow \dfrac{{BX}}{{DY}} = \dfrac{2}{1} - - - (6)\]
Dividing \[(6)\] by \[(3)\], we get
\[ \Rightarrow \dfrac{{\left( {\dfrac{{BX}}{{DY}}} \right)}}{{\left( {\dfrac{{EX}}{{DY}}} \right)}} = \dfrac{{\left( {\dfrac{2}{1}} \right)}}{{\left( {\dfrac{1}{2}} \right)}}\]
On solving,
\[ \Rightarrow \dfrac{{BX}}{{EX}} = \dfrac{4}{1}\]
On simplification,
\[ \Rightarrow BX = 4EX\]
As \[BX = BE + EX\], we can write the above equation as
\[ \Rightarrow BE + EX = 4EX\]
Taking \[EX\] from L.H.S. to R.H.S.
\[ \Rightarrow BE = 4EX - EX\]
\[ \Rightarrow BE = 3EX\]
On rearranging,
\[ \Rightarrow \dfrac{{BE}}{{EX}} = \dfrac{3}{1}\]
Hence, proved that \[BE:EX = 3:1\].

Note:
We have to find the ratio of \[BE:EX\], we are not interested in the exact value of \[BE\] and \[EX\]. Here we used the concept of similarity because it gives relation between ratios of different sides. As when two triangles are similar, their corresponding sides are proportional.