Question

Given D, E and F are respectively the midpoints of the sides BC, CA, and AB of a triangle ABC. Show that,
(i) BDEF is a parallelogram
\[\left( ii \right)area\left( DEF \right)=\dfrac{1}{4}area\left( ABC \right)\]
\[\left( iii \right)area\left( BDEF \right)=\dfrac{1}{2}area\left( ABC \right)\]

Answer 1

Hint: First, draw a diagram of the given situation. To prove part (i), use the midpoint theorem given as “if we join midpoints of any two sides of a triangle then this line is parallel to the third side of the triangle and its length is equal to half the length of this third side”. To prove part (ii), first, prove that the triangle ABC is divided into four congruent triangles whose areas are the same. Use the result obtained in part (i). Similarly, prove part (iii) by considering the properties of congruent triangles.

Complete step by step answer:
Here, we have been given a triangle ABC with D, E, and F as the midpoints of the sides BC, CA, and AB respectively. We have been asked to prove three relations provided in the question. But first, let us draw a diagram of the given situation.

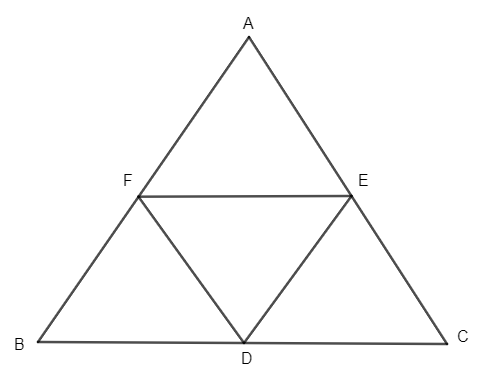
Let us consider each part of the question one by one.
(i) Here, we need to prove that BDEF is a parallelogram.
Now since D, E and F are the midpoints, therefore we know that the midpoint theorem states that “the line joining the midpoints of two sides of a triangle is parallel to the third side and its length is equal to half of the length of the third side.” So, we have,
FF parallel to BC and hence BD also.
DE parallel to AB and hence BF also.
So, we can say that the opposite sides of the quadrilateral BDEF are parallel to each other, which is a property of the parallelogram.
Hence, BDEF is a parallelogram.
\[\left( ii \right)area\left( DEF \right)=\dfrac{1}{4}area\left( ABC \right)\]
Now, in the figure, we can clearly see that DF is the diagonal of the parallelogram BDEF and we know that the diagonal of a parallelogram divides it into two congruent triangles. So, we have,
\[\Delta DEF\cong \Delta FBD.......\left( i \right)\]
Similarly, we can prove that,
\[\Delta DEF\cong \Delta EDC.......\left( ii \right)\]
\[\Delta DEF\cong \Delta AFE.......\left( iii \right)\]
Therefore, from equations (i), (ii) and (iii), we can say that all the four small triangles are congruent to each other. We know that the areas of the congruent triangles are also equal. So, we have,
\[\Rightarrow Area\left( DEF \right)=Area\left( FBD \right)=Area\left( EDC \right)=Area\left( AFE \right)......\left( iv \right)\]
Now, we can see that the triangle ABC is made up of all the triangles noted in equation (iv). So, we have,
\[\Rightarrow 4Area\left( DEF \right)=Area\left( ABC \right)\]
\[\Rightarrow Area\left( DEF \right)=\dfrac{1}{4}Area\left( ABC \right)\]
Hence proved.
\[\left( iii \right)area\left( BDEF \right)=\dfrac{1}{2}area\left( ABC \right)\]
Now, we can see that the parallelogram is made up of two congruent triangles given by equation (i). So, we have,
\[\Rightarrow Area\left( BDEF \right)=2Area\left( DEF \right)\]
Using the result obtained in part (ii), we get,
\[\Rightarrow Area\left( BDEF \right)=2\times \dfrac{1}{4}Area\left( ABC \right)\]
\[\Rightarrow Area\left( BDEF \right)=\dfrac{1}{2}Area\left( ABC \right)\]
Hence proved.
Therefore, all the results are proved.

Note:
One may note that there are many other methods to prove all the three given results. In part (i), we can also prove that the opposite sides of the quadrilateral are equal to prove it a parallelogram. In part (ii), we can prove that the triangle ABC and DEF are similar by A-A-A (angle-angle – angle) similarity criteria to get the result. You may note that all the parts of the question are interconnected, so use the results obtained in the previous parts to get the new results. Remember the midpoint theorem and properties of the parallelogram to solve the question.