Question

Give the order the rotational symmetry for each figure.

Answer 1

Hint: Rotational symmetry, also known as radial symmetry, is the property a shape has when it looks the same after some rotation by a particular turn. An object degree of rotational symmetry is the number of distinct orientations in which it looks exactly the same for each rotation

Complete step-by-step answer:
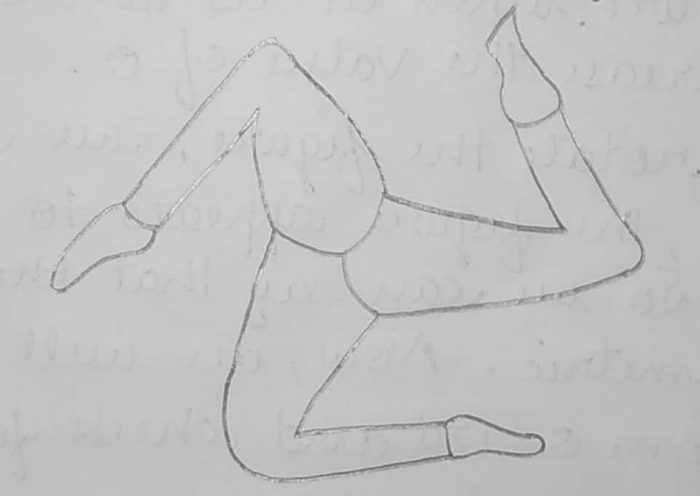
In the above question, we have to find the order of rotational symmetry for the figure given. The order of rotational symmetry for a figure given the order of rotational symmetry of a shape is the number of times it can be rotated around a full circle and still look the same. For example, if a shape gains its original shape n times when it is rotated through \[{{360}^{o}}\]its order will be n. In the above question, we have to rotate the figure step by step till it appears to look the same.
We assume that initially the figure is not rotated with respect to original position. Let \[\theta \] be the angle through which we are rotating the figure. Initially \[\theta ={{0}^{o}}\], now we will increase the value of \[\theta \] gradually and check at which value of \[\theta \], it looks the same as the figure. When it is at \[\theta ={{0}^{o}}\]. Now we are going to increase the value of \[\theta \].
When we will rotate the figure, we come to known that at \[\theta ={{120}^{o}}\], the figures appears to be same as figure at \[\theta ={{0}^{o}}\]. So, we can say that the figure is rotationally symmetric. Now, we will again increase the value of \[\theta \] from \[\theta ={{120}^{o}}\] and check for symmetry. At \[\theta ={{240}^{o}}\], again the figure appears to be the same as the figure at \[\theta ={{0}^{o}}\]. Now, we will again increase the value of \[\theta \] gradually. Again, we will note that at \[\theta ={{360}^{o}}\], the figure becomes rotationally symmetric to the figure at \[\theta ={{0}^{o}}\]. So, in \[0<\theta \le {{360}^{o}}\], the figure becomes rotationally symmetric to the figure at \[\theta ={{0}^{o}}\] three times. So, the order of the figure given in question is 3.


Note: The shortcut trick for finding the order of a given figure is described as: -
First we find the lowest angle which is rotationally symmetric to the figure at \[\theta ={{0}^{o}}\]. Let this angle be \[\varnothing \]. Now the order of this figure will be = \[\dfrac{{{360}^{o}}}{\varnothing (in\deg ree)}\].