
Give the justification of the following construction:
Draw a line segment of length 7.6 cm and divide it in the ratio $5:8$. Measure the two parts.
Answer
591k+ views
Hint: We will first draw the line segment of the given length then we will draw a ray and then we will add the given ratios that are $5:8$ and divide the ray into that many parts. After we will join the endpoints of the ray and the line segment and draw a parallel line from the fifth partition and hence, get the required ratio.
Complete step-by-step solution
First of all, draw AB of length 7.6 cm:
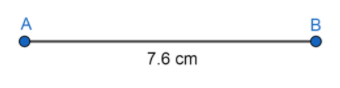
Now, draw any ray AX which makes an acute angle with AB, which means that angle should be less than ${{90}^{\circ }}$ :
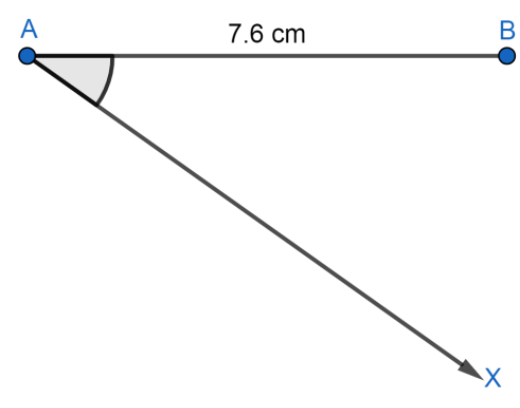
Now, we are given the ratio $5:8$so we will mark 13 points on it as $5+8=13$. So, let the 13 points will be: ${{A}_{1}},{{A}_{2}},{{A}_{3}}............{{A}_{13}}$ on AX such that: $A{{A}_{1}}={{A}_{1}}{{A}_{2}}={{A}_{2}}{{A}_{3}}.........$ by drawing equal arcs as follows:
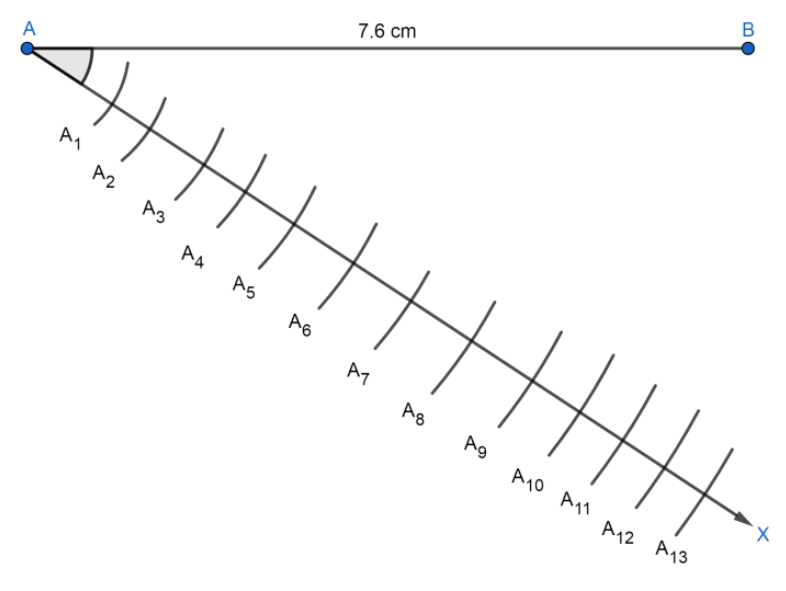
Now, we will join $B{{A}_{13}}$, which will look like the following:
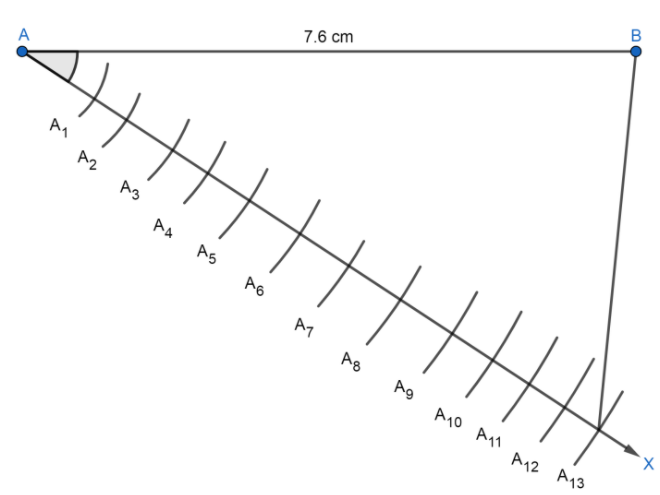
Since we want the ratio $5:8$, now we will draw a line parallel to $B{{A}_{13}}$. Now, we will draw a line parallel to $B{{A}_{13}}$ by making $\angle A{{A}_{5}}B=\angle A{{A}_{13}}C$ which we will look like the following:
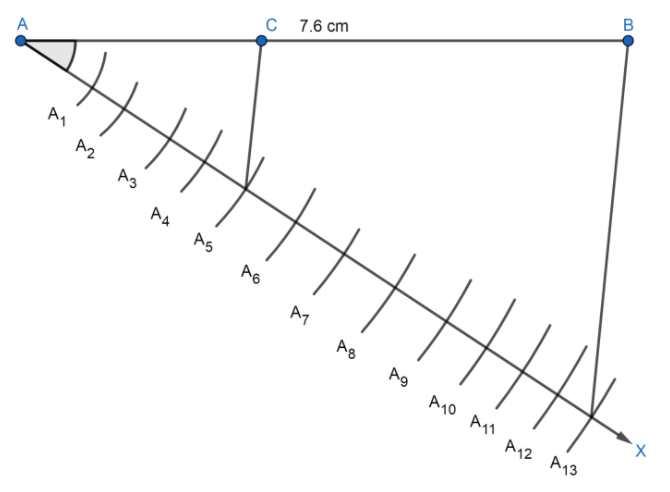
Thus, the ratio of $AC:CB=5:8$, now we will measure AC and BC by the scale and we will get:
$AC=2.9\text{ cm and BC}=4.7\text{ cm}$ .
Now, let’s look at the justification of this construction:
Since, $\angle A{{A}_{5}}B=\angle A{{A}_{13}}C$, therefore for lines ${{A}_{13}}B$ and ${{A}_{5}}C$ with AX as transversal, which means corresponding angles are equal.
Therefore: ${{A}_{13}}B\parallel {{A}_{5}}B$ . Now, by basic proportionality theorem: $\dfrac{A{{A}_{5}}}{{{A}_{5}}{{A}_{13}}}=\dfrac{AC}{CB}$
When we measure ${{A}_{5}}C$ and ${{A}_{13}}B$ :
Therefore, we will get:
$\dfrac{A{{A}_{5}}}{{{A}_{5}}{{A}_{13}}}=\dfrac{5}{8}\Rightarrow \dfrac{A{{A}_{5}}}{{{A}_{5}}{{A}_{13}}}=\dfrac{5}{8}=\dfrac{AC}{CB}$
Thus, C divides AB in the ratio: $5:8$
Note: Be careful while drawing the graphs and it can be a bit confusing. Student can make a mistake while first dividing 7.6 cm into the given ratios $5:8$ first, $\dfrac{7.6}{13}\times 5=2.92\text{ and }\dfrac{7.6}{13}\times 8=4.7$ and then construct the given statement which gives us the given line segment, but that won’t be correct as we are required to construct the line segment and then divide it.
Complete step-by-step solution
First of all, draw AB of length 7.6 cm:

Now, draw any ray AX which makes an acute angle with AB, which means that angle should be less than ${{90}^{\circ }}$ :

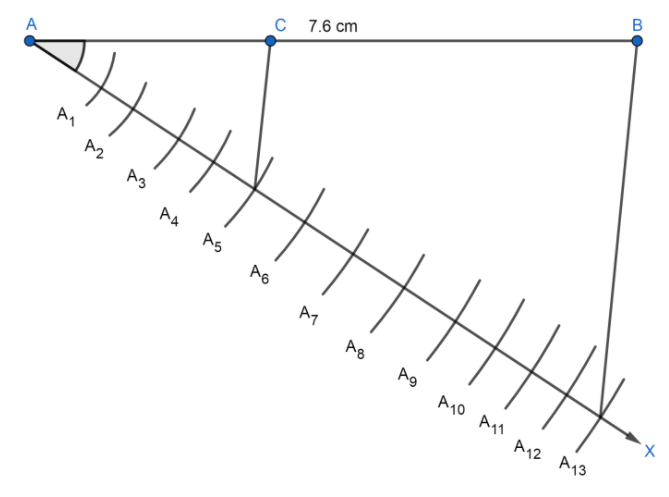
Now, we are given the ratio $5:8$so we will mark 13 points on it as $5+8=13$. So, let the 13 points will be: ${{A}_{1}},{{A}_{2}},{{A}_{3}}............{{A}_{13}}$ on AX such that: $A{{A}_{1}}={{A}_{1}}{{A}_{2}}={{A}_{2}}{{A}_{3}}.........$ by drawing equal arcs as follows:

Now, we will join $B{{A}_{13}}$, which will look like the following:

Since we want the ratio $5:8$, now we will draw a line parallel to $B{{A}_{13}}$. Now, we will draw a line parallel to $B{{A}_{13}}$ by making $\angle A{{A}_{5}}B=\angle A{{A}_{13}}C$ which we will look like the following:

Thus, the ratio of $AC:CB=5:8$, now we will measure AC and BC by the scale and we will get:
$AC=2.9\text{ cm and BC}=4.7\text{ cm}$ .
Now, let’s look at the justification of this construction:
Since, $\angle A{{A}_{5}}B=\angle A{{A}_{13}}C$, therefore for lines ${{A}_{13}}B$ and ${{A}_{5}}C$ with AX as transversal, which means corresponding angles are equal.
Therefore: ${{A}_{13}}B\parallel {{A}_{5}}B$ . Now, by basic proportionality theorem: $\dfrac{A{{A}_{5}}}{{{A}_{5}}{{A}_{13}}}=\dfrac{AC}{CB}$
When we measure ${{A}_{5}}C$ and ${{A}_{13}}B$ :

Therefore, we will get:
$\dfrac{A{{A}_{5}}}{{{A}_{5}}{{A}_{13}}}=\dfrac{5}{8}\Rightarrow \dfrac{A{{A}_{5}}}{{{A}_{5}}{{A}_{13}}}=\dfrac{5}{8}=\dfrac{AC}{CB}$
Thus, C divides AB in the ratio: $5:8$
Note: Be careful while drawing the graphs and it can be a bit confusing. Student can make a mistake while first dividing 7.6 cm into the given ratios $5:8$ first, $\dfrac{7.6}{13}\times 5=2.92\text{ and }\dfrac{7.6}{13}\times 8=4.7$ and then construct the given statement which gives us the given line segment, but that won’t be correct as we are required to construct the line segment and then divide it.
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Class 10 Question and Answer - Your Ultimate Solutions Guide

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
Who is known as the "Little Master" in Indian cricket history?

Explain the Treaty of Vienna of 1815 class 10 social science CBSE

A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

The highest dam in India is A Bhakra dam B Tehri dam class 10 social science CBSE

Describe the process of Unification of Italy class 10 social science CBSE

Who Won 36 Oscar Awards? Record Holder Revealed




