Question

Give the derivation for resultant of two vectors and for the angle between resultant and a vector.

Answer 1

Hint: In this question, we will first construct the given vectors and thereby it’s resultant. Then we will further use the Pythagoras theorem and also we will use the basic trigonometry to solve and get the required result. Further, we will see the basics of vectors, for our better understanding.

Formula used:
 ${H^2} = {B^2} + {P^2}$
$\cos \theta = \dfrac{{base}}{{hypotenuse}}$
$\sin \theta = \dfrac{{perpendicular}}{{hypotenuse}}$
$\tan \phi = \dfrac{{perpendicular}}{{base}}$

Complete step by step solution:
Let us assume P and Q is the given two vectors acting simultaneously at a given point. Also, both the given vectors are represented in magnitude and direction by two adjacent sides given as OA and OD of a parallelogram OABD as shown in figure below:

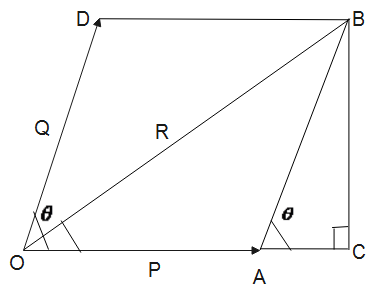
Now, let $\theta $ be the angle between the given vectors P and Q. Here, R is the resultant vector. So, as we know from the parallelogram law of vector addition, which gives that diagonal OB represents the resultant of P and Q.

So, from above we have:
R=P+Q

Now, by expanding A to C and drawing BC perpendicular to OC, we construct a triangle OCB:
$O{B^2} = {C^2} + B{C^2}$
$O{B^2} = {(OA + AC)^2} + B{C^2}...........(1)$

Now, in triangle ABC, we have:
$\cos \theta = \dfrac{{AC}}{{AB}}$
$\eqalign{
  & \Rightarrow AC = AB\cos \theta \cr
  & \Rightarrow AC = OD\cos \theta \cr
  & \Rightarrow AC = Q\cos \theta ..........(AB = OD = Q) \cr} $

Also we have,
$\sin \theta = \dfrac{{BC}}{{AB}}$
$\eqalign{
  & \Rightarrow BC = AB\sin \theta \cr
  & \Rightarrow BC = OD\sin \theta \cr
  & \Rightarrow BC = Q\sin \theta .............(AB = OD = Q) \cr} $

Now, we will find the magnitude of the resultant vector:
So, by substituting the value of AC and BC from above results in equation ( 1 ), we get:
${R^2} = {(P + Q\cos \theta )^2} + {(Q\sin \theta )^2}$
${R^2} = P{}^2 + 2PQ\cos \theta + {Q^2}{\cos ^2}\theta + {Q^2}{\sin ^2}\theta $
$ \Rightarrow {R^2} = P{}^2 + 2PQ\cos \theta + {Q^2}$
$ \Rightarrow R = \sqrt {P{}^2 + 2PQ\cos \theta + {Q^2}} $

Now we find the direction of the given resultant R :
Let $\phi $ be the angle made by resultant R with the vector P.
So, from the triangle OBC, we get:
$\tan \phi = \dfrac{{BC}}{{OC}} = \dfrac{{BC}}{{OA + AC}}$
$\eqalign{& \tan \phi = \dfrac{{Q\sin \theta }}{{P + Q\cos \theta }} \cr
  & \therefore \phi = {\tan ^{ - 1}}\left( {\dfrac{{Q\sin \theta }}{{P + Q\cos \theta }}} \right) \cr} $

This is the required expression for direction of resultant vector R.

Therefore, we get the required magnitude and direction of resultant vector R.

Additional information:
As we know that, ordinary quantities that have a magnitude but not direction are called scalars. Example: speed, time.

Also, a vector quantity is known as the quantity having magnitude and direction. Vector quantities must obey certain rules of combination.
These rules are:

VECTOR ADDITION: it is written symbolically as A + B = C. So, that it completes the triangle. Also, If A, B, and C are vectors, it should be possible to perform the same operation and achieve the same result i.e., C, in reverse order, B + A = C.

VECTOR MULTIPLICATION: This is the other rule of vector manipulation i.e., multiplication by a scalar- scalar multiplication. It is also termed as the dot product or inner product, and also known as the cross product.

If we take example: we already know the basic difference of speed and velocity i.e., speed is the measure of how fast an object can travel, whereas velocity tells us the direction of this speed. As we know speed is a scalar quantity that means speed has only magnitude not direction, whereas velocity is a vector quantity that means that velocity has both magnitude and direction as well. The S.I unit of velocity is meter per second (m/sec).

Note:
We should remember that vectors have both magnitude and direction as well, whereas the scalar has only magnitude not direction. Also, we should know that vectors can be used to find the angle of the resultant vector from its parent vectors.