Question

From time to time, when grain storage is limited farmers will store grain in conical piles in their fields. Depending on how long the grain remains in these piles, the grain may be left uncovered or will be covered with a tarp. Wheat will form a conical pile with an angle of \[25^\circ \] between the slant side and the horizontal (ground). This angle is called the angle of repose. The angle of repose varies from one kind of grain to another. Corn, for example, has a \[22^\circ \] angle of repose.
Suppose a conical pile of wheat is 3 m in height. What is the length of the slant side of the conical pile? Round your answer to one decimal place.

Answer 1

Hint:
Here we have to find the slant side of the conical pile. For that, we will draw the right angled triangle that is located inside the cone whose base is equal to the radius of the cone and the slant height of the cone is its hypotenuse. We will then use the sine angle formula of the right angled triangle to find the required slant height of the cone.

Complete step by step solution:
Let’s first draw the given cone with given height 3m and angle between the slant height and the base is \[25^\circ \].

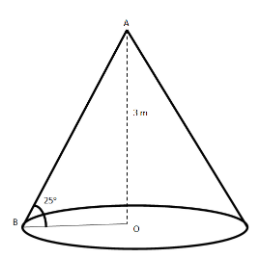
We will extract the triangle from the cone with the vertices as A, B, O.
Let’s draw the triangle now.

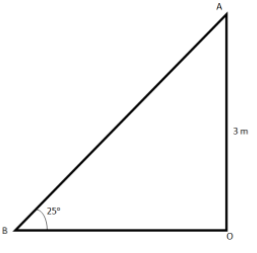
Triangle AOB is a right angled triangle. \[AO = 3m\] and \[\angle ABO = 25^\circ \]
We will use the sine angle formula now.
\[sin\theta = \dfrac{{{\rm{perpendicular}}}}{{{\rm{hypotenuse}}}}\]
Substituting \[\theta = 25^\circ \], perpendicular\[ = 3\] in the above formula, we get
\[sin25^\circ = \dfrac{3}{{AB}}\]
We know the value of \[sin25^\circ \]is \[0.4226\].
Now substituting the value of \[sin25^\circ \] in the above equation, we get
\[0.4226 = \dfrac{3}{{AB}}\]
Cross multiplying the terms, we get
\[AB = \dfrac{3}{{0.4226}}\]
Simplifying the fraction, we get
\[AB = 7.098m\]

Hence the length of the required slant side of the cone is \[7.098\] m.

Note:
We have used the sine function to find the slant height of the cone. Sine function is defined as the ratio of the side of a right angled triangle which is opposite to the given angle to the longest side of the right angled triangle i.e. the hypotenuse.
Slant height of a cone is defined as the length of the line joining the point of vertex of the cone and the point on the circumference of the base of the cone.