
From the top of the lighthouse of height 200 feet, the lighthouse keeper observes a Yacht and a Barge along the same line of sight. The angles of depression for the Yacht and the Barge are ${{45}^{\circ }}$ and ${{30}^{\circ }}$ respectively. For safety purposes, the two sea vessels should be at least 300 feet apart. If they are less than 300 feet, the keeper has to sound the alarm. Does the keeper have to sound the alarm?
Answer
580.5k+ views
Hint: To find whether the keeper has to sound the alarm, we have to find the distance between Yacht and Barge. We will draw a figure using the given data.
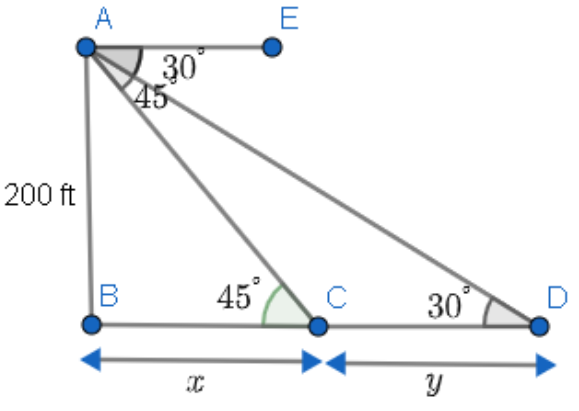
We will find $x$ , that is the distance of Yacht from lighthouse, from triangle ABC using the formula $\tan {{45}^{\circ }}=\dfrac{\text{AB}}{\text{BC}}=\dfrac{\text{200}}{x}$ . Similarly, we can find the value of $y$ , that is the distance between Yacht and Barge, from triangle ABD using $\tan {{30}^{\circ }}=\dfrac{\text{AB}}{\text{BD}}=\dfrac{\text{200}}{x+y}$ . Solving this, we will get the value of $y$ . If $y<300\text{ ft}$ , the keeper has to sound the alarm.
Complete step-by-step solution
We have to find out whether the keeper has to sound the alarm. For this, we have to find the distance between the Yacht and Barge. Let us draw a figure with the given data.
It is given that the height of the lighthouse $AB=200\text{ ft}$.
$\angle EAD$ is the angle of depression for the Barge is $\angle EAC$ is the angle of depression for the Yacht.
We have $\angle EAD={{30}^{\circ }}$ . Hence, $\angle DAC={{30}^{\circ }}$ as they are vertically opposite angles.
Similarly, we have $\angle EAC={{45}^{\circ }}$ . Hence, $\angle ACB={{45}^{\circ }}$ as they are vertically opposite angles.
Let us consider $x$ to be the distance of Yacht from the lighthouse and \[y\] to be the distance of Barge from Yacht.
Let us consider the triangle ABC.
We know that for a right triangle,
$\tan \theta =\dfrac{\text{Opposite side}}{\text{Adjacent side}}$
$\Rightarrow \tan {{45}^{\circ }}=\dfrac{\text{AB}}{\text{BC}}$
From figure, we can write the above form as
$\tan {{45}^{\circ }}=\dfrac{\text{200}}{x}$
We know that $\tan {{45}^{\circ }}=1$ . Hence, the above form becomes
$1=\dfrac{\text{200}}{x}$
Let us now solve this.
$x=200\text{ ft}...(i)$
Let us now consider the triangle ABD.
We have,
$\tan {{30}^{\circ }}=\dfrac{\text{AB}}{\text{BD}}$
From figure, we can write the above form as
$\tan {{30}^{\circ }}=\dfrac{\text{200}}{x+y}$
We know that $\tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}}$ . Hence, the above form becomes
$\dfrac{1}{\sqrt{3}}=\dfrac{\text{200}}{x+y}$
Using (i), we can write the above equation as
$\dfrac{1}{\sqrt{3}}=\dfrac{\text{200}}{200+y}$
Let us solve this.
$\begin{align}
& 200+y=200\sqrt{3} \\
& \Rightarrow y=200\sqrt{3}-200 \\
\end{align}$
Taking the common term outside from LHS, we will get
$y=200\left( \sqrt{3}-1 \right)$
$\begin{align}
& \Rightarrow y=200\left( 1.732-1 \right) \\
& \Rightarrow y=200\left( 0.732 \right) \\
& \Rightarrow y=146.4\text{ ft} \\
\end{align}$
It is given that if the two vessels are less than 300 feet, that is, the distance between Yacht and Barge, the alarm will be initiated. We have found that $y=146.4\text{ ft}$ , that is, the distance of Barge from Yacht is $146.4\text{ ft}$. We know that,
$y<300\text{ ft}$ .
Hence, the keeper has to sound the alarm.
Note: When drawing the diagram, be careful that Yacht is closer to the lighthouse not the Barge. Also, be aware that in the question, the angle of depression is given not elevation. You may make an error when writing the formula $\tan \theta =\dfrac{\text{Opposite side}}{\text{Adjacent side}}$ as $\tan \theta =\dfrac{\text{Adjacent side}}{\text{Opposite side}}$ .

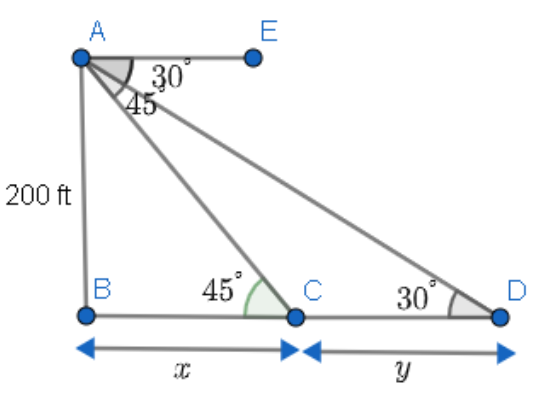
We will find $x$ , that is the distance of Yacht from lighthouse, from triangle ABC using the formula $\tan {{45}^{\circ }}=\dfrac{\text{AB}}{\text{BC}}=\dfrac{\text{200}}{x}$ . Similarly, we can find the value of $y$ , that is the distance between Yacht and Barge, from triangle ABD using $\tan {{30}^{\circ }}=\dfrac{\text{AB}}{\text{BD}}=\dfrac{\text{200}}{x+y}$ . Solving this, we will get the value of $y$ . If $y<300\text{ ft}$ , the keeper has to sound the alarm.
Complete step-by-step solution
We have to find out whether the keeper has to sound the alarm. For this, we have to find the distance between the Yacht and Barge. Let us draw a figure with the given data.

It is given that the height of the lighthouse $AB=200\text{ ft}$.
$\angle EAD$ is the angle of depression for the Barge is $\angle EAC$ is the angle of depression for the Yacht.
We have $\angle EAD={{30}^{\circ }}$ . Hence, $\angle DAC={{30}^{\circ }}$ as they are vertically opposite angles.
Similarly, we have $\angle EAC={{45}^{\circ }}$ . Hence, $\angle ACB={{45}^{\circ }}$ as they are vertically opposite angles.
Let us consider $x$ to be the distance of Yacht from the lighthouse and \[y\] to be the distance of Barge from Yacht.
Let us consider the triangle ABC.
We know that for a right triangle,
$\tan \theta =\dfrac{\text{Opposite side}}{\text{Adjacent side}}$
$\Rightarrow \tan {{45}^{\circ }}=\dfrac{\text{AB}}{\text{BC}}$
From figure, we can write the above form as
$\tan {{45}^{\circ }}=\dfrac{\text{200}}{x}$
We know that $\tan {{45}^{\circ }}=1$ . Hence, the above form becomes
$1=\dfrac{\text{200}}{x}$
Let us now solve this.
$x=200\text{ ft}...(i)$
Let us now consider the triangle ABD.
We have,
$\tan {{30}^{\circ }}=\dfrac{\text{AB}}{\text{BD}}$
From figure, we can write the above form as
$\tan {{30}^{\circ }}=\dfrac{\text{200}}{x+y}$
We know that $\tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}}$ . Hence, the above form becomes
$\dfrac{1}{\sqrt{3}}=\dfrac{\text{200}}{x+y}$
Using (i), we can write the above equation as
$\dfrac{1}{\sqrt{3}}=\dfrac{\text{200}}{200+y}$
Let us solve this.
$\begin{align}
& 200+y=200\sqrt{3} \\
& \Rightarrow y=200\sqrt{3}-200 \\
\end{align}$
Taking the common term outside from LHS, we will get
$y=200\left( \sqrt{3}-1 \right)$
$\begin{align}
& \Rightarrow y=200\left( 1.732-1 \right) \\
& \Rightarrow y=200\left( 0.732 \right) \\
& \Rightarrow y=146.4\text{ ft} \\
\end{align}$
It is given that if the two vessels are less than 300 feet, that is, the distance between Yacht and Barge, the alarm will be initiated. We have found that $y=146.4\text{ ft}$ , that is, the distance of Barge from Yacht is $146.4\text{ ft}$. We know that,
$y<300\text{ ft}$ .
Hence, the keeper has to sound the alarm.
Note: When drawing the diagram, be careful that Yacht is closer to the lighthouse not the Barge. Also, be aware that in the question, the angle of depression is given not elevation. You may make an error when writing the formula $\tan \theta =\dfrac{\text{Opposite side}}{\text{Adjacent side}}$ as $\tan \theta =\dfrac{\text{Adjacent side}}{\text{Opposite side}}$ .
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




