Question

From the top of Cliff $ 25{\text{ m}} $ height. The angle of elevation of the top of the tower is found to be equal to the angle of depression of the foot of the tower. The height of the tower is

Answer 1

Hint: The knowledge of application of trigonometry is used in this question. The value of tangent of the angle of depression and elevation should be used to calculate the height of the tower. If a person stands and looks up at an object, the angle of elevation is the angle between the horizontal line of sight and the object. If a person stands and looks down at an object, the angle of depression is the angle between the horizontal line of sight and the object.

Complete step-by-step answer:
Given information is
The height of the cliff, $ h = 25{\text{ m}} $ .
The angle of the elevation of the top of the tower is equal to the angle of depression of the bottom of the tower from the top of the cliff.

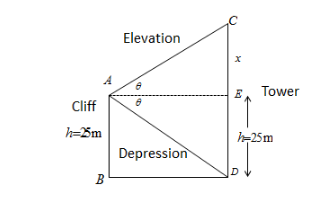
The diagram according to the condition given in the question is shown above.
Let the angle of elevation and angle of depression be equal to $ \theta $ and the height of the tower is CD.
The value of CD as per the figure above can be written as,
 $ CD = CE + ED \cdots \left( 1 \right) $
The value of ED is equal to the height of the cliff as $ ED = 25{\text{ m}} $ (as per the figure both are straight and parallel lines).
Now we are only required to determine CE.
Let the value of CE be $ x $ .
Hence, the value of CD can be written as
 $ CD = x + 25 \cdots \left( 2 \right) $
In triangle , right angled at E.
 $
\Rightarrow \tan \theta = \dfrac{x}{{AE}} \\
\Rightarrow x = AE \times \tan \theta \cdots \left( 3 \right) \\
  $
In triangle $ \Delta AED $ , right angled at E
 $
\Rightarrow \tan \theta = \dfrac{{25}}{{AE}} \\
\Rightarrow 25 = AE \times \tan \theta \cdots \left( 4 \right) \\
  $
Equating equation (3)a and equation (4) ,we get
 $\Rightarrow x = 25{\text{ m}} $ .
Substitute the value of $ x = 25 $ in equation (2) to calculate the height of the tower
 $
\Rightarrow h = 25 + 25 \\
\Rightarrow h = 50{\text{ m}} \;
  $
Thus, the height of the tower is $ 50{\text{ m}} $ .
So, the correct answer is “$ 50{\text{ m}} $”.

Note: The important point is to draw the figure correctly. Once the figure is drawn correctly the value for the tower can be calculated easily.
The value of the tangent of the angle is given as,
 $ \tan \theta = \dfrac{{Perpendicular}}{{base}} $