Question

From the top of a tower of height $40\,m$, a ball is projected upwards with a speed of $20\,m{s^{ - 1}}$ at an angle of elevation of $30^\circ $. The ratio of the total time taken by the ball to hit the ground to its time of flight (time taken to come back to the same elevation) is:
A. 2:1
B. 1:2
C. 1:1
D. 3:2

Answer 1

Hint: in order to solve the question, we will first use the formula of time of flight then we will find value of total time taken by the balls to hit the ground by the using the relation between velocity, distance and time after then we will compare the time taken by the balls to hit the ground and the time of flight to find the ratio

Formula used:
$T = \dfrac{{2V\sin \theta }}{g}$
Where, $T$ is time of flight and $V$ is the velocity.
${\text{time = }}\dfrac{{{\text{distance}}}}{{{\text{velocity}}}}$

Complete step by step answer:
In the question we are given that from the top of a tower, a ball is projected upwards and we have to find the ratio of the total time taken by the ball to hit the ground to its time of flight (time taken to come back to the same elevation)
Height of the tower = $40\,m$
Speed of ball = $20\,m{s^{ - 1}}$
Angle of elevation = $30^\circ $.

To find the time of flight we will use the formula of time of flight that is
$T = \dfrac{{2V\sin \theta }}{g}$
Velocity as given in question is 20 $m{s^{ - 1}}$ value of theta is given which makes it easier to find the $\sin \theta $, g is constant value of g in this question is ( $g = 10m{s^{ - 2}}$)
Substituting the values in the equation of time of flight
$T = \dfrac{{2 \times 20m{s^{ - 1}} \times \sin 30^\circ }}{{10m{s^{ - 1}}}}$
Substituting the value of $\sin 30^\circ = \dfrac{1}{2}$
$T = \dfrac{{2 \times 20m{s^{ - 1}} \times \dfrac{1}{2}}}{{10m{s^{ - 1}}}}$
$\Rightarrow T = 2\,sec$
Hence the value of time of flight is 2 sec.

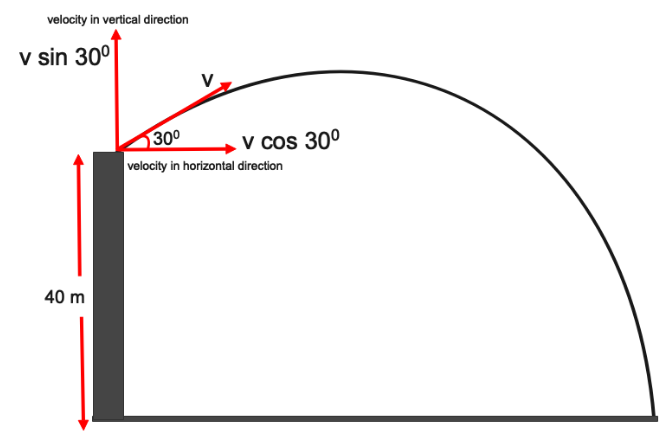
Now we have to find the value of total time taken by the balls to hit the ground using the relation between velocity, time and distance. Now applying the velocity applied in the vertical direction.
Velocity = $20\sin 30^\circ $
Distance that it has to cover in vertical direction is the height of tower which is equal to 40 m
${\text{time = }}\dfrac{{{\text{distance}}}}{{{\text{velocity}}}}$
Substituting the values
${\text{time = }}\dfrac{{40}}{{20\sin 30^\circ }}\sec $
Substituting the value of $\sin 30^\circ = \dfrac{1}{2}$
Time = 4 sec
Hence the value of total time taken by the balls to hit the ground is 4 sec. Taking the ratio of value of total time taken by the balls to hit the ground and the time of flight.
So, the ratio is 4 sec:2 sec = 2:1

Hence, the correct option is A.

Note:Many of the students may confuse what we have taken into consideration to find the value of total time taken by the balls to hit the ground it is the measure of the time which ball covers when it goes upward and downward which is vertical motion and doesn’t involve the horizontal motion and it’s velocity and range.