Question

From the top of a building $ 50\sqrt 3 m $ high, the angle of depression of an object on the ground is observed to be $ 45^\circ . $ Find the distance of the object from the building.

Answer 1

Hint: Convert the word problem into mathematical equations. Use trigonometric ratios to solve it. If we observe its Isosceles right angle triangle and the value of tan45 is 1.

Complete step-by-step answer:
Let us consider the building as \[AB\], and consider the object as \[C\]

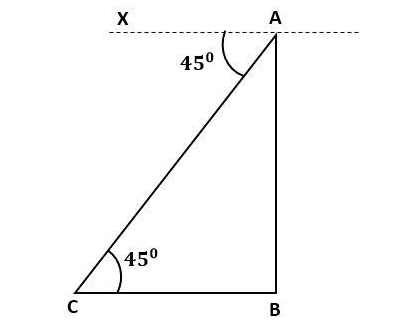
It is given that, angle of depression is $ {45^0} $
 $ \Rightarrow \angle XAC = {45^0} $
Since, alternate interior angles of two parallel lines are equal, we get
 $ \angle ACB = {45^0} $ $ \left( {\because AX||BC} \right) $
It is given that, the height of the building, $ AB = 50\sqrt 3 m $
Now, in a $ \Delta ABC $
 $ \tan C = \dfrac{{AB}}{{BC}} $
 $ \Rightarrow \tan {45^0} = \dfrac{{50\sqrt 3 }}{{BC}} $ $ \left( {\because AB = 50\sqrt 3 m} \right) $
 $ \Rightarrow 1 = \dfrac{{50\sqrt 3 }}{{BC}} $ $ \left( {\because \tan {{45}^0} = 1} \right) $
By cross multiplying, we get
 $ BC = 50\sqrt 3 m $
Therefore, the distance of object from the building is $ 50\sqrt 3 m $

Note: It can also be solved in short. A right angled triangle, whose one angle is $ {45^0} $ must be isosceles triangle.
 $ \Rightarrow AB = BC = 50\sqrt 3 m $