Question

From the top of a 50 m high tower, the angles of the depression of the top and bottom of a pole are observed to $45{}^\circ \text{ and 60}{}^\circ $ respectively. Find the height of the pole.

Answer 1

Hint: First draw a rough diagram of the given conditions. Now, assume that the height of the pole is ‘h’ and its distance from the tower is ‘d’. Form two equations in ‘h’ and ‘d’ using the information provided and solve these two equations to get the value of ‘h’ and ‘d’. Use $\tan \theta =\dfrac{\text{perpendicular}}{\text{base}}$ to form the equations in the right angle triangle.

Complete step-by-step answer:
Let us assume that P is the bottom of the pole and Q is the top of the pole. It is given that the top of the tower is denoted by B and bottom as A. So, let us draw the diagram of the given situation.

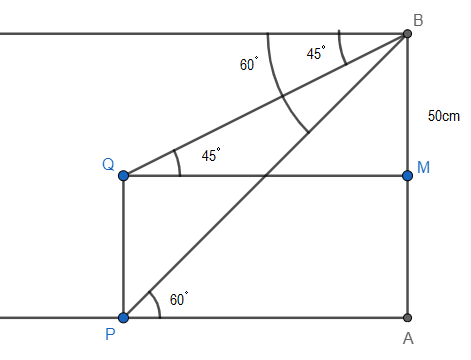
From the above figure, we have,
In right angle triangle PAB,
AP = d, AB = h
\[\angle APB=60{}^\circ \] , as from the figure we can see that angle of depression of the bottom of the pole are alternate interior angles, and alternate interior angles are equal.
Therefore, using $\tan \theta =\dfrac{\text{perpendicular}}{\text{base}}$, we have,
$\begin{align}
  & \tan 60{}^\circ =\dfrac{AB}{AP} \\
 & \Rightarrow \tan 60{}^\circ =\dfrac{50}{d} \\
 & \Rightarrow d=\dfrac{50}{\tan 60{}^\circ }........................(i) \\
\end{align}$
Now, in right angle triangle BQM,
QM = AP = d, as they are the opposite sides of the rectangle PAMQ.
BM = AB – AM = 50-h , because it is given that the height of the tower is 50m and here we have assumed the tower as AB.
Also, \[\angle BQM=45{}^\circ \] , as from the figure we can see that angle of depression of the top of the pole are alternate interior angles, and alternate interior angles are equal.
Therefore, using $\tan \theta =\dfrac{\text{perpendicular}}{\text{base}}$, we have,
$\begin{align}
  & \tan 45{}^\circ =\dfrac{BM}{QM} \\
 & \Rightarrow \tan 45{}^\circ =\dfrac{50-h}{d} \\
 & \Rightarrow 50-h=d\tan 45{}^\circ \\
 & \Rightarrow h=50-d\tan 45{}^\circ .........................(ii) \\
\end{align}$
Now if we put the value of d from equation (i), we get
$\begin{align}
  & \\
 & h=50-\dfrac{50\tan 45{}^\circ }{\tan 60{}^\circ } \\
\end{align}$
We know that $\tan 45{}^\circ =1\text{ and tan60}{}^\circ \text{=}\sqrt{3}$ .
$\begin{align}
  & \\
 & h=50-\dfrac{50}{\sqrt{3}} \\
\end{align}$
$\Rightarrow h=\dfrac{50\left( \sqrt{3}-1 \right)}{\sqrt{3}}$
Therefore, the height of the pole is $\dfrac{50\left( \sqrt{3}-1 \right)}{\sqrt{3}}meters$ .

Note: We must substitute and eliminate the variables properly otherwise we may get confused while solving the equations. Here, in the above question we have used the tangent of the given angle because we have to find both, height of the tower and its distance from the post. So, the function relating these two variables is tangent of the angle.