Question

From the top and foot of a 40m high tower, the angle of elevation of the top of lighthouse are found to be ${{30}^{\circ }}$ and ${{60}^{\circ }}$ respectively. Find the height of the lighthouse.

Answer 1

Hint: We will first use trigonometric equations to find the distance between the tower and the lighthouse, and then use that value to find the length of the lighthouse.

Complete step by step answer:

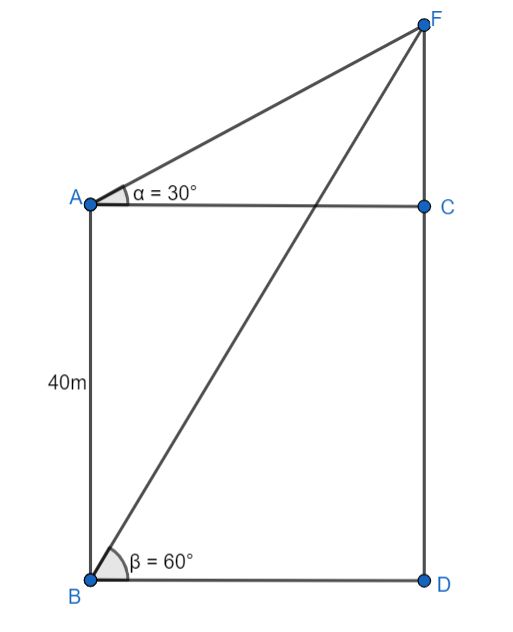
Let us consider AB to be a tower of length 40m, then AB=AC=40m. Let FD be the lighthouse.
Here, the angle of elevation from top of the tower to top of the lighthouse is ${{30}^{\circ }}$, that is, $\angle FAC={{30}^{\circ }}$. And, angle of elevation from the foot of the tower to the top of lighthouse is ${{60}^{\circ }}$, that is, $\angle FBD={{60}^{\circ }}$.
Let us consider the length of AC to be $x$, then the length of BC is also $x$, as can be seen from the diagram.
Let the length of FC be $y$.
Now, from basic definition of trigonometry, we have,
$\tan A=\dfrac{p}{b}$.
Using this in $\Delta AFC$, we get,
$tan(\angle FAC)=\dfrac{\text{FC}}{\text{AF}}$
where, $\angle FAC={{30}^{\circ }}$, $FC=y,\,AC=x$.
Therefore, $\tan {{30}^{\circ }}=\dfrac{y}{x}$.
Also, $\tan {{30}^{\circ }}=\dfrac{1}{2}$. Using this value in above equation, we get,
 $\dfrac{1}{\sqrt{3}}=\dfrac{y}{x}$
Cross multiplying this, we get,
$x=\sqrt{3}y\cdots \cdots \left( i \right)$
Again, in $\Delta BFD$
$tan(\angle BFD)=\dfrac{\text{FD}}{\text{BF}}$
where, $\angle BFD={{60}^{\circ }}$, $FD=FC+CD=y+40\text{m}\,\,\text{and}\,AC=x$.
Therefore, $\tan {{60}^{\circ }}=\dfrac{y+40\text{m}}{x}$
Also, $\tan {{60}^{\circ }}=\sqrt{3}$. Using this value in above equation, we get,
 $\sqrt{3}=\dfrac{y+40\text{m}}{x}$
Cross multiplying this, we get,
$\sqrt{3}x=y+40m$
Putting value of $x$ from equation $\left( i \right)$ here, we get,
$\sqrt{3}\times \sqrt{3}y=y+40\text{m}$
Multiplying root terms, we get,
$\begin{align}
  & \Rightarrow 3y=y+40\text{m} \\
 & \Rightarrow 3y-y=40\text{m} \\
 & \Rightarrow 2y=40\text{m} \\
\end{align}$
Dividing 2 on both sides of the equation, we get,
$\begin{align}
  & y=\dfrac{40}{2}\text{m} \\
 & \Rightarrow y=20\text{m} \\
\end{align}$
Therefore, height of the lighthouse is given by,
 \[\begin{align}
  & \text{FD = FC+CD}=\,\left( y+40 \right)\text{m} \\
 & =\left( 20+40 \right)\text{m} \\
 & =60\text{m} \\
\end{align}\]
Hence, the height of the lighthouse is 60m.

Note: In this question, while drawing diagrams, pay attention that both the angles are taken from the tower, not one from the tower and one from the lighthouse. And both angles are meeting at the same point. Also, the distance between tower and lighthouse remains the same at all heights.