Question

From the given figure, find the value of x.

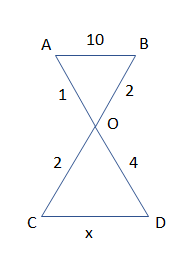
(a) 20
(b) 5
(c) 4
(d) 10

Answer 1

Hint: First, before proceeding for this, we must know the property of triangles that if all the angles of the triangles are equal and the sides of the triangle are in the same ratio then we can say that both triangles are similar. Then, we get all the angles of the triangles ABO and CDO as equal. Then, we get another condition that if these two triangles are similar then the third side should be having the same ratio as the other two sides which is $\dfrac{1}{2}$.

Complete step by step answer:

In this question, we are supposed to find the value of x from the given figure as:

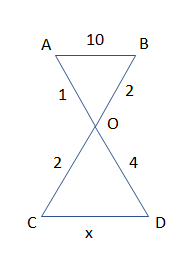
So, before proceeding for this, we must know the property of triangles that if all the angles of the triangles are equal and the sides of the triangle are in the same ratio then we can say that both triangles are similar.
So, from the figure, we can clearly see that:
$\angle AOB=\angle COD$(vertically opposite angles)
$\angle OAB=\angle ODC$(alternate interior angles)
$\angle OCD=\angle OBA$(alternate interior angles)
So, we get all the angles of the triangles ABO and CDO as equal.
Then, we can see clearly that the ratio of the triangle ABO and CDO is also same as:
$\dfrac{OA}{OC}=\dfrac{OB}{OD}$
So, by substituting their values, we can confirm that whether they have same ratio or not as:
$\begin{align}
  & \dfrac{1}{2}=\dfrac{2}{4} \\
 & \Rightarrow \dfrac{1}{2}=\dfrac{1}{2} \\
\end{align}$
So, we get that both the triangles have the same ratio.
So, by using the above-stated property of triangles that if all the angles are equal and side are in the same ratio then triangles are similar gives triangle ABO is similar to triangle CDO.
Now, we get another condition that if these two triangles are similar then the third side should be having the same ratio as the other two sides which is $\dfrac{1}{2}$.
So, by using it, we get the relation as:
$\dfrac{AB}{CD}=\dfrac{1}{2}$
Now, by substituting the value of AB as 10 and CD as x from the figure, we get:
$\begin{align}
  & \dfrac{10}{x}=\dfrac{1}{2} \\
 & \Rightarrow 2\times 10=x\times 1 \\
 & \Rightarrow x=20 \\
\end{align}$
So, we get the value of x as 20.
Hence, option (a) is correct.

Note:
Now, to solve these types of questions we need to know some of the basics of the similarity of the triangles as it is most necessary in these types of questions to proceed further. Moreover, sometimes the triangle looks like but if they are not matching the condition of similarity so never consider them similar before proving it.