Question

From any point $P$ on the ellipse, $PN$ is drawn perpendicular to the $x$ axis and produced to $Q$, so that $NQ$ equals $PS$, where $S$ is a focus. Prove that the locus of $Q$ is the two straight lines
\[y\pm ex+a=0\].

Answer 1

Hint: First, make sure you draw the diagram of the ellipse, as this is a general problem without any values given, so it will be very convenient to get confused otherwise. Next, remember the equations of the directrices and the foci of the ellipse, and proceed to make use of the distance of point $P$ from either of the two foci and the directrices to find the eccentricity of the ellipse. This will make the question easier to tackle.

Complete step-by-step answer:
Let’s assume an ellipse \[\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\]

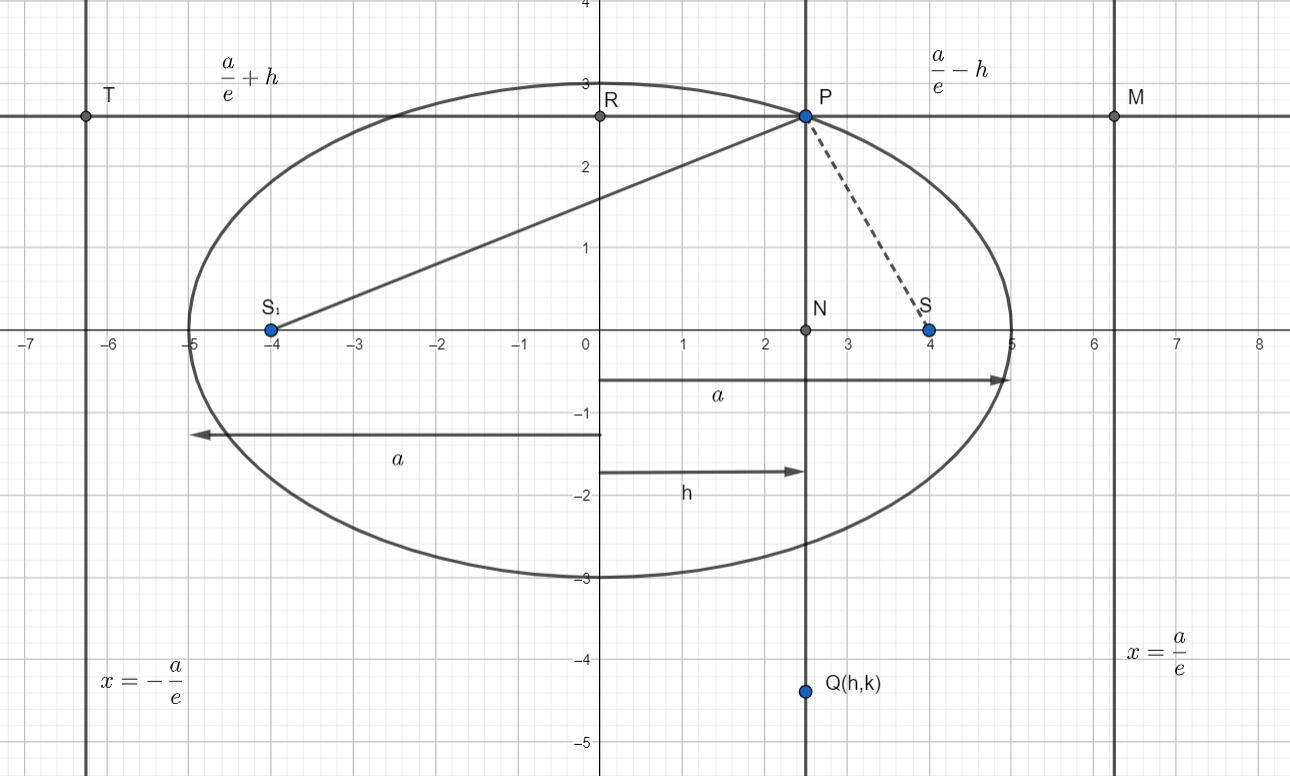
\[S\,\,and\,\,{{S}_{1}}\]are foci of the ellipse.
\[x=\dfrac{a}{e}\,\,and\,\,x=-\dfrac{a}{e}\,\] are directrix of the ellipse.
According to the question let’s assume a point $P$ on the ellipse and draw a perpendicular on the $x$axis with at $N$ and extend up to a point $Q$.
Let co-ordinates of the point\[Q\equiv (h,k)\].
From the above diagram,
The horizontal distance of point $Q$ from the $y$ axis \[=h\] (because $h$ is the $x$ coordinate of point $Q$).
\[MR=\dfrac{a}{e}\]
\[PM=MR-RP\]
\[\therefore PM=\dfrac{a}{e}-h\] ………… (A)
Similarly,
$\begin{align}
  & RT=\dfrac{a}{e} \\
 & PT=PR+TR \\
 & \Rightarrow PT=\dfrac{a}{e}+h \\
\end{align}$
\[PT=\dfrac{a}{e}+h\] ……………. (B)
From the definition of an ellipse
Eccentricity \[e=\dfrac{PS}{PM}=\dfrac{P{{S}_{1}}}{PT}\] ………. (1)
From the expression (1)
\[\begin{align}
  & PS=ePM \\
 & \Rightarrow PS=e\left( \dfrac{a}{e}-h \right)=a-eh \\
\end{align}\] (From A) ………… (2)
\[\begin{align}
  & P{{S}_{1}}=ePT \\
 & \Rightarrow P{{S}_{1}}=e\left( \dfrac{a}{e}+h \right) \\
\end{align}\] (From B) ………… (3)
Now, given that
The absolute value of $NQ$= Absolute value of $PS$ or $P{{S}_{1}}$
Since the segment $NQ$ is below the $x$ axis.
\[NQ=PS\,\,or\,\,P{{S}_{1}}\]
\[NQ=|k|\] , Because $k$ is $y$coordinate of point $Q$.
Distance
\[\Rightarrow PS\,=a-eh\] from eq. (2)
\[\Rightarrow P{{S}_{1}}\,=a+eh\] from eq. (3)
\[\Rightarrow k\,=a\pm eh\]
\[\Rightarrow k\,\pm eh-a=0\]
Therefore; the locus of the point $Q$ with co-ordinates\[(h,k)\], can be formed by replacing\[(h,k)\to (x,y)\].
\[\therefore y\,\pm ex-a=0\].
Note: Ellipse is the locus of a point which moves in a plane such that the ratio of its distance from a fixed straight line always remains constant and that constant value is known as eccentricity .