Question

From an external point P, two tangents, PA and PB are drawn to a circle with centre O. At one point E on the circle tangent is drawn which intersects PA and PB at C and D, respectively. If PA = 10 cm, find the perimeter of the triangle PCD in cm.

Answer 1

Hint: In order to solve this problem we need to draw the diagram and use the concept that two tangents on the circle from an external point are equal in length.

Complete step-by-step answer:
The figure of the above problem can be drawn as:

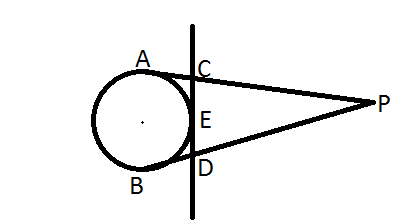
From the figure:
PA = 10cm (Given)
We need to find the perimeter of triangle PCD.
PA = PB = 10cm (Two tangents on the circle from an external point are equal in length.)
If we carefully watch out we get to know that there are two tangents from C and two from D.
So, we can also say that DB = DE and CA = CE…………….(1)
And we can write CD = CE + ED = DB + CA……………(2)
Now the perimeter of the triangle PCD is:
PC + CD + PD = PC + CA + DB + PD (From (1) and (2))
But if we consider diagram we get to know that:
PC + CA = PA and PD + DB = PB……………(3)
So, the perimeter PC + CA + DB + PD = PA + PB (From (3))
But PA = PB = 10cm
So, PA +PB = 10cm +10cm =20cm = Perimeter of the triangle PCD.
Hence the answer is 20cm.

Note: To solve such questions of circle one need to draw the diagram carefully and then observe it as well. Here we have found the perimeter by using the concept of length of tangents being equal from an external point. Students sometimes try to use the radius of the circle here for a solution as the radius is perpendicular to the tangent but it does not give you the solution to this problem. This is the one and only way to solve it.