Question

From a wooden cylindrical block, whose diameter is equal to its height, a sphere of the maximum possible volume is carved out. What is the ratio of the volume of the utilized wood to that of the wasted wood?

Answer 1

Hint: To find the ratio of the volume of the utilized wood to that of the wasted wood. Let us first find the volume of the block, we will first find the volume of wood, that is, the cylinder using the formula $\pi {{r}^{2}}h$. It is given that the height of the cylinder and diameter are the same. Hence, volume of wood $=2\pi {{r}^{3}}$ . Now, we will find the volume of utilized wood, that is, the sphere. We will use the formula $=\dfrac{4}{3}\pi {{r}^{3}}$ . The volume of wasted wood is obtained by subtracting the volume of utilized wood from the volume of the total wood $\dfrac{2\pi {{r}^{3}}}{3}.$. Dividing $\dfrac{4}{3}\pi {{r}^{3}}$ by $\dfrac{2\pi {{r}^{3}}}{3}.$ , the required ratio can be computed.

Complete step-by-step solution
We need to find the ratio of the volume of the utilized wood to that of the wasted wood. Let us first find the volume of the block. We know that the block is in the form of a cylinder. We have,
Volume of cylinder $=\pi {{r}^{2}}h$
It is given that the height of the cylinder and diameter are the same.

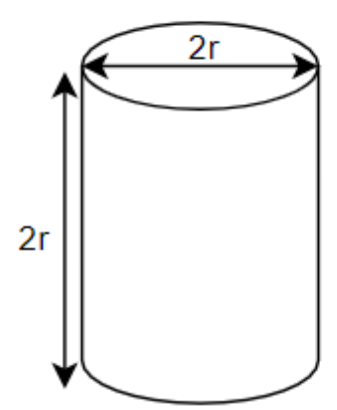
Hence, we have
$h=D$
We know that the diameter is twice the radius. Hence,
$D=2r$
Now, we can write the volume of the cylinder as
Volume of cylinder $=\pi {{r}^{2}}\times 2r=2\pi {{r}^{3}}$
It is given that a sphere of the maximum possible volume is carved out from this cylinder. Hence, the radius of the sphere will be the same as that of the cylinder.
Now, we can write the volume of the sphere. It is given as
Volume of sphere $=\dfrac{4}{3}\pi {{r}^{3}}$

This will be the volume of utilized wood. Hence,
Volume of utilized wood $=\dfrac{4}{3}\pi {{r}^{3}}...(i)$
Let us find the volume of wasted wood. This is done by subtracting the volume of utilized wood from the volume of the total wood (that is volume of cylinder). We can write this as
Volume of wasted wood $=2\pi {{r}^{3}}-\dfrac{4}{3}\pi {{r}^{3}}$
Let us now solve this. We will get
Volume of wasted wood $=\dfrac{6\pi {{r}^{3}}-4\pi {{r}^{3}}}{3}=\dfrac{2\pi {{r}^{3}}}{3}...(ii)$
We have to find the ratio of the volume of the utilized wood to that of the wasted wood. This is done by dividing (i) by (ii). That is,
Required ratio $=\dfrac{\dfrac{4}{3}\pi {{r}^{3}}}{\dfrac{2\pi {{r}^{3}}}{3}}$
Let us now cancel the denominators. We will get
Required ratio $=\dfrac{4\pi {{r}^{3}}}{2\pi {{r}^{3}}}$
By canceling the common terms, we will get
Required ratio $=\dfrac{2}{1}=2:1$
Hence, the ratio of the volume of the utilized wood to that of the wasted wood is 2:1.

Note: You may make a mistake when writing the formula for the volume of cylinder as $2\pi rh$. This is the curved surface area of the cylinder. You may also make an error when writing the formula for the volume of the sphere as $4\pi {{r}^{2}}$. It is the area of the sphere. Also, be careful when finding the required ratio. Do not divide the volume of the wasted wood into that of the utilized wood.