Question

From a window (60m high above the ground) of a house in a street, the angles of elevation and depression of the top and foot of the another house on the opposite side of the street are ${{60}^{\circ }},{{45}^{\circ }}$ respectively. Show that the height of the opposite house is $60\left( 1+\sqrt{3} \right)m$.

Answer 1

Hint: Draw a neat diagram with the given information of the problem and represent all the distances and angles. Now, observe the diagram and apply the trigonometric functions in the right angled triangles. Use identity:
$\tan \theta =\left( \dfrac{\text{perpendicular}}{\text{base}} \right)$ and values of $\tan {{45}^{\circ }},\tan {{60}^{\circ }}$ are 1, $\sqrt{3}$ respectively.

Complete step-by-step answer:
So, the informations given in the problem are:
(i) Angle of elevation from a window of a house to another house is ${{60}^{\circ }}$ to the top.
(ii) Angle of depression from the window of the same house to another is ${{45}^{\circ }}$to the foot.
(iii) Height of the window of the first house from where angles of depression and elevation is given, is 60m.
Now, we can draw a neat diagram with the help of the above informations as

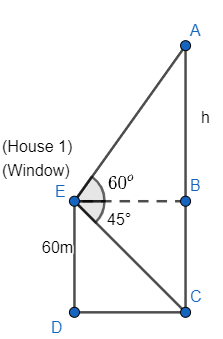
Now, we can relate from the above diagram that AC is the height of the second house to which the angle of elevation and depression from the window of another house is observed.
As DC is a line on the ground that is respectively the distance between the feet of the houses, so it will be perpendicular to the lines representing the height of the houses. And hence BCDE will be a rectangle as two angles C and D are ${{90}^{\circ }}$and ED and BC are parallel to each other. Hence all the other angles of quadrilateral BCDE will be ${{90}^{\circ }}$and opposite sides will be equal in length and parallel to each other. So, we get $\angle EBC=\angle BCD=\angle CDE=\angle DEB={{90}^{\circ }}$.
It means $\angle ABE$ will also be ${{90}^{\circ }}$ as $\angle ABE,\angle BCE$ are linear pairs and lying on a line CA so, sum of them will be ${{180}^{\circ }}$; hence $\angle ABE+\angle CBE={{180}^{\circ }}$, So, we get
$\begin{align}
  & 90+\angle ABE=180 \\
 & \angle ABE={{90}^{\circ }} \\
\end{align}$
It means $\Delta ABE$ is a right angle triangle.
So, now, we get from the above symmetries observed in the diagram as
DC = EB ………………. (i)
BC = ED = 60m ………………… (ii)
$\angle ABE={{90}^{\circ }}$ ………………… (iii)
Now, in $\Delta EBC$, we get
$\begin{align}
  & \tan \left( \angle CEB \right)=\left( \dfrac{perpendicular}{base} \right) \\
 & \tan \left( {{45}^{\circ }} \right)=\dfrac{BC}{EB} \\
\end{align}$
Put values of $\tan {{45}^{\circ }}$and BC as 1 and 60m to the above equation as BC = 60m from equation (ii). So, we get
$1=\dfrac{60}{EB}$
Or
EB = 60m …………………… (iv)
Now, in $\Delta ABE$, we get
$\begin{align}
  & \tan \left( \angle AEB \right)=\dfrac{\text{perpendicular}}{\text{base}} \\
 & \tan {{60}^{\circ }}=\dfrac{h}{EB} \\
\end{align}$
Put the values of $\tan {{60}^{\circ }}$and EB as $\sqrt{3}$ and 60m respectively, as value of EB is 60m
$\sqrt{3}=\dfrac{h}{60}$
$h=60\sqrt{3}m$ …………………. (v)
We know that we need to determine the height of the house (2) i.e. the length AC. So, length AC is given as summation of lengths of AB and BC. So, we get
AC = AB + BC
We know values of AB and BC as $h=60\sqrt{3}m$ from the equation (v) and BC = 60m from equation (ii) respectively. So, we get length AC as
$\begin{align}
  & AC=60\sqrt{3}+60 \\
 & AC=60\left( \sqrt{3}+1 \right)m \\
\end{align}$
Hence, it is shown that the height of the opposite house is $60\left( \sqrt{3}+1 \right)m$.

Note: One can use ‘$\tan $’, ‘$\cot $’ functions with the triangles EBC and ABE. As we do not need the hypotenuses side of them. So, don’t apply any other trigonometric functions with the triangles and don’t confuse with the definitions of trigonometric functions as well. As solutions will be flexible and move easier by applying $\tan ,\cot $ functions. Another approach for the question would be that we can find the sides AB and EC by applying $\cos {{60}^{\circ }},\sin {{45}^{\circ }}$in triangles ABE and BCE respectively and hence apply cosine formula in the triangle ACE. As we know
$\cos \theta =\dfrac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc}$
Where a, b, c are sides of a triangle and $\theta $ is the angle between ‘b’ and ‘c’. so, we can apply this identity as well with any of the angles of $\angle CAE,\angle ACE$. We know $\angle CAE={{30}^{\circ }},\angle ACE={{45}^{\circ }}$ by the fundamental property of the triangle that sum of interior angles of a triangle is ${{180}^{\circ }}$. So, it can be another approach.