Question

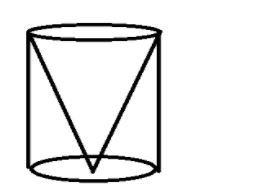
From a solid right circular cylinder of a height 2.4cm and radius of 0.7cm,a right circular cone of same height and same radius is cut. Find the total surface area of the remaining solid.

Answer 1

Hint: To solve such a type of question we need to analyze the type of figure formed at last and then find the surface area of the remaining figure by dividing it in terms of different figures.

Complete step-by-step answer:
Given,
Height of a cylinder = 2.4cm
Radius of cylinder = 0.7cm
Height of cone=2.4cm
Radius of cone=0.7cm
Total surface area of the remaining solid= curved surface area of cylinder + area of base+ curved surface area of cone
Curved surface area of cylinder=$2\pi rh$
$
   \Rightarrow 2 \times \dfrac{{22}}{7} \times (0.7) \times (2.4) \\
   \Rightarrow 10.55c{m^2} \\
$
Area of base=$\pi {r^2}$
$
   = (\dfrac{{22}}{7}) \times {(0.7)^2} \\
   = 1.53c{m^2} \\
$
Slant height of cone, $l = \sqrt {{r^2} + {h^2}} $
$
  l = \sqrt {{{(0.7)}^2} + {{(2.4)}^2}} \\
  l = \sqrt {6.25} \\
  l = 2.5cm \\
$
Curved surface area of cone=$\pi rl$
$
   = (\dfrac{{22}}{7}) \times (0.7) \times 2.5 \\
   = 5.49c{m^2} \\
$
Total surface area of the remaining solid = curved surface area of cylinder + area of base+ curved surface area of cone
Total surface area=10.55+1.53+5.49
=17.57 $c{m^2}$
Hence the answer to this question is 17.57 $c{m^2}$.

Note: To solve such a question we must remember the surface area of the figure required to be calculated and their formulae and later sum them up to obtain the total surface area of the solid. Doing this will solve your problem.