Question

From a point on the bridge across a river, the angle of depression of the banks on the opposite sides of the river are ${{30}^{o}}$ & ${{45}^{o}}$ respectively. If the bridge is at a height of 3m from the bank, then find the width of the river?

Answer 1

Hint: We start solving the problem by drawing all the given information. We then recall the definition of tangent of angle in a given triangle We use this fact to find the distance between the point and the bank at which the angle of depression is ${{30}^{o}}$. Similarly, we also use tangents of the angle ${{45}^{o}}$ to find the distance between the point and the other bank. We then add these distances to find the width of the river.

Complete step by step answer:
According to the problem, we have given that the angle of depression of the banks on the opposite sides of the river are ${{30}^{o}}$ & ${{45}^{o}}$. We need to find the width of the river if the height of the bridge is given as 3m.
Let us draw the given information to get a better view.

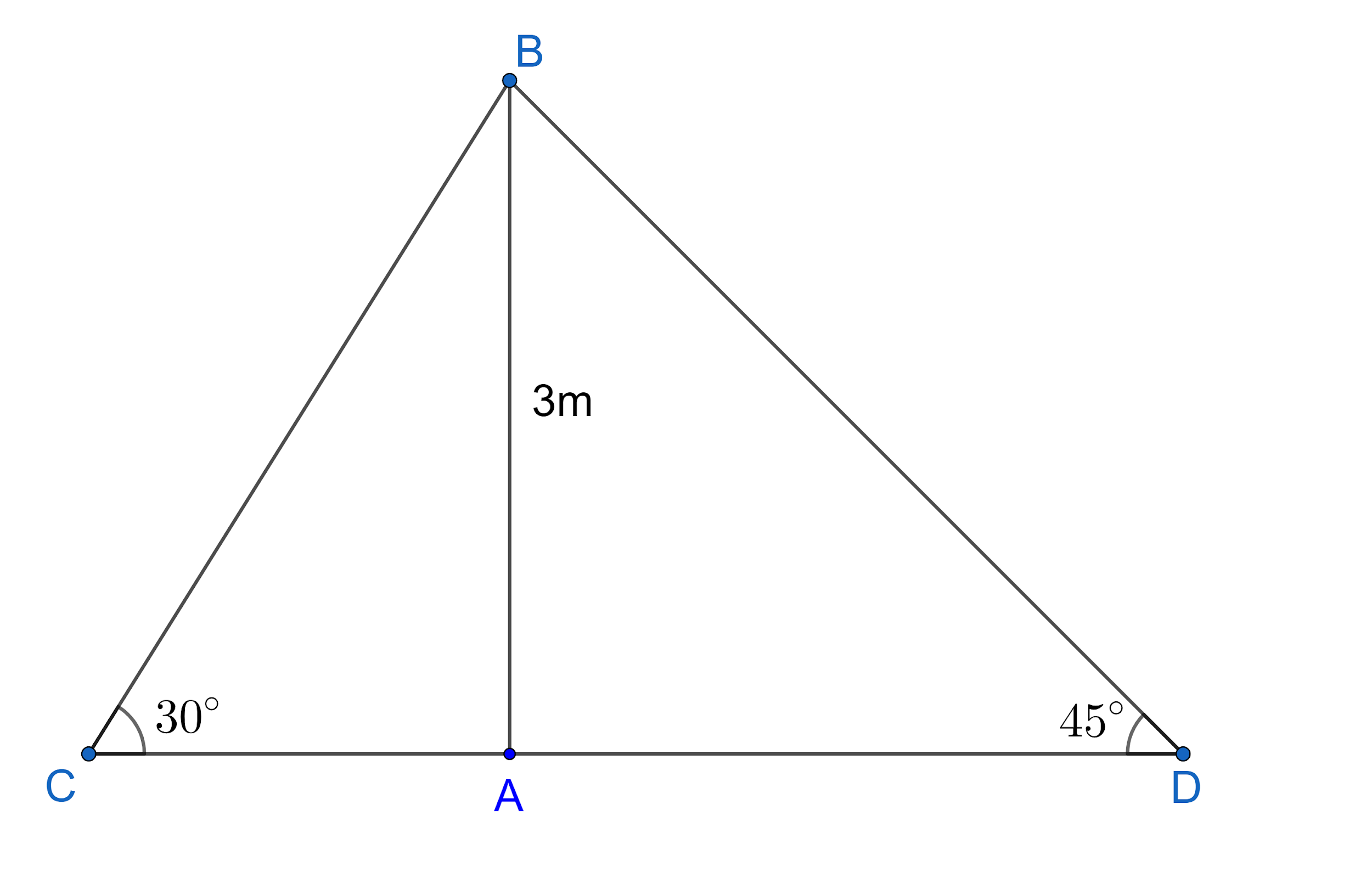
Let us assume ‘A’ be the point on the bridge, AB be the height of the bridge and CD be the width of the river.
We know that tangent of an angle in a right-angled triangle is defined as $\tan \theta =\dfrac{\text{opposite side}}{\text{adjacent side}}$
.
From the triangle ABC, we have $\tan {{30}^{o}}=\dfrac{AB}{CA}$.
$\Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{3}{CA}$.
$\Rightarrow CA=3\sqrt{3}$m ---(1).
From the triangle ABD, we have $\tan {{45}^{o}}=\dfrac{AB}{AD}$.
$\Rightarrow 1=\dfrac{3}{AD}$.
$\Rightarrow AD=3$m ---(2).
From the figure, we can see that the sum of the lengths of CA and AD is equal to the length of the CD. So, we have $CD=CA+AD$.
From equations (1) and (2), we get $CD=\left( 3\sqrt{3}+3 \right)m$.
$\Rightarrow CD=3\left( \sqrt{3}+1 \right)m$.
So, we have found the width of the river as $3\left( \sqrt{3}+1 \right)m$.
The width of the river is $3\left( \sqrt{3}+1 \right)m$.

Note:
We can also find all the angles of the triangle and find the length of the sides of the triangle using the sine law of triangles. Whenever we get this type of problem, we better start with drawing all the information so that all the calculations will become easier. We should not make calculation mistakes while applying tangent to the angle and finding the length of the sides of triangles.