Question

From a disc of radius $R$ and mass $M$, a circular hole of diameter $R$, whose rim passes through the centre is cut. What is the moment of inertia of the remaining part of the disc about a perpendicular axis, passing through the centre?
A) $\dfrac{15M{{R}^{2}}}{32}$
B) $\dfrac{13M{{R}^{2}}}{32}$
C) $\dfrac{11M{{R}^{2}}}{32}$
D) $\dfrac{9M{{R}^{2}}}{32}$

Answer 1

Hint: Moment of inertia of a disc is equal to half the product of mass of the disc and the square of radius of the disc. Parallel axis theorem states that the moment of inertia of a body about an axis parallel to the body passing through its centre is equal to the sum of moment of inertia of body about the axis passing through the centre and product of mass of the body times the square of distance between the two axes.

Complete step by step answer:
Moment of inertia of a body is a quantity which expresses the body’s tendency to resist angular acceleration. For a disc, it is equal to half the product of mass of the disc and the square of radius of the disc. From the question, we are told that a small disc of diameter $R$ is cut out from a disc of mass $M$ and radius $R$ in such a way that the rim of the cut out disc passes through the centre of the big disc. Let us call the mass of the small disc ${{M}_{1}}$ and radius of the small disc ${{R}_{1}}$. This is shown in figure 1.

Figure 1

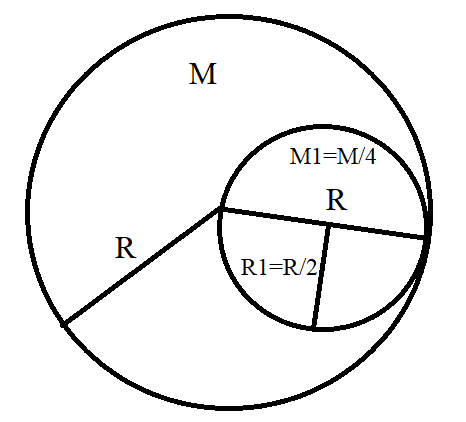
For the big disc, from which the small disc is cut out, let the moment of inertia be given by ${{I}_{total}}$. It is clear from the definition that
${{I}_{total}}=\dfrac{1}{2}M{{R}^{2}}$
where
$M$ is the mass of the big disc and $R$ is the radius of the big disc.
Let this be equation 1.
Now, we are asked to find the moment of inertia about a perpendicular axis of the remaining part of the big disc after the small disc is cut out from it. Let us call this moment of inertia ${{I}_{remain}}$. Let us also name the moment of inertia of the small disc ${{I}_{1}}$. Clearly,
${{I}_{remain}}={{I}_{total}}-{{I}_{1}}$
Let this be equation 2.
Now, let us find the moment of inertia of the small disc ${{I}_{1}}$.
We have to use the parallel axis theorem here because the axis of the small disc is parallel to the axis of the big disc. Parallel axis theorem states that the moment of inertia of a body about an axis parallel to the body passing through its centre is equal to the sum of moment of inertia of body about the axis passing through the centre and product of mass of the body times the square of distance between the two axes i.e.
${{I}_{1}}={{I}_{c}}+{{M}_{1}}R_{1}^{2}$
where
${{I}_{c}}$ is the moment of inertia at the centre of the small disc.
${{M}_{1}}$ is the mass of the small disc
${{R}_{1}}$ is the radius of the small disc
Let this be equation 3.
Let us calculate ${{I}_{c}}$ first. We know that mass of a disc is proportional to its area. Therefore, ${{M}_{1}}$ can be written as
${{M}_{1}}=\dfrac{M}{4}$
where $M$is the mass of the big disc
Also, as provided in the question,
${{R}_{1}}=\dfrac{R}{2}$
where $R$is the radius of the big disc
The moment of inertia at the centre of the small disc is given by
${{I}_{c}}=\dfrac{1}{2}{{M}_{1}}R_{1}^{2}=\dfrac{1}{2}\left( \dfrac{M}{4} \right){{\left( \dfrac{R}{2} \right)}^{2}}=\dfrac{M{{R}^{2}}}{32}$
Now, let us substitute these values equation 3.
${{I}_{1}}={{I}_{c}}+{{M}_{1}}R_{1}^{2}=\dfrac{M{{R}^{2}}}{32}+\left( \dfrac{M}{4} \right){{\left( \dfrac{R}{2} \right)}^{2}}=\dfrac{M{{R}^{2}}}{32}+\dfrac{M{{R}^{2}}}{16}=\dfrac{3M{{R}^{2}}}{32}$
Let this be equation 4.
Moving on, let us substitute the values of equation 1 and equation 4 in equation 2. We have
${{I}_{remain}}={{I}_{total}}-{{I}_{1}}=\dfrac{1}{2}M{{R}^{2}}-\dfrac{3M{{R}^{2}}}{32}=\dfrac{13M{{R}^{2}}}{32}$
Therefore, the moment of inertia of the remaining disc about a perpendicular axis passing through the centre, after the small disc is cut out from the big disc is equal to
${{I}_{remain}}=\dfrac{13M{{R}^{3}}}{32}$

Hence, the correct option is B.

Note:
In this question, we are required to find the moment of inertia of the remaining part of the disc about a perpendicular axis passing through the centre. From this, we can understand that the axis of the small disc, which is cut out, has an axis parallel to the big disc. In such a case, we have to use the parallel axis theorem. Students might have the tendency to use perpendicular axis theorem just because they see the word perpendicular axis in the question. Clearly understanding the question can easily sort out such problems.