
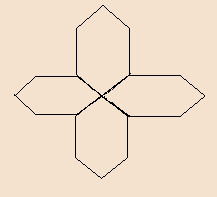
Four regular hexagons are drawn so as to form the design as shown. If the perimeter of the design is $28{\text{ cm}}$. Find the length of each side of the hexagon.

Answer
584.4k+ views
Hint:
Assume the length of each side of the design to be a cm as a regular hexagon has an equal number of sides. Now count the number of sides of the design. Then use the formula-
The perimeter of regular hexagon = number of sides × length of the side
Now put the values of perimeter and number of sides in the formula and solve the obtained function to get the answer.
Complete step by step solution:
Given, four regular hexagons are drawn as shown below-
The perimeter of the design=$28{\text{ cm}}$
We have to find the length of each side of the hexagon.
A regular hexagon has equal sides and equal angles. So, all the sides of the given design have equal sides. Let the length of one side is a cm.
According to the arrangement of hexagons, the number of sides=$14$
Now we know that perimeter is the sum of all sides of the polygon.
So we can write, the perimeter of given regular hexagon = number of sides × length of the side
On putting the values of perimeter, length, and number of sides we get-
$ \Rightarrow 28 = 14 \times a$
On adjusting, we get-
$ \Rightarrow a = \dfrac{{28}}{{14}}$
On division, we get-
$ \Rightarrow a = 2$
Hence the length of each side of the hexagon is $2{\text{ cm}}$.
Note:
The properties of a regular hexagon are-
1) It has six sides and six angles.
2) All the sides and measures of angles are equal to each other.
3) The regular hexagon has total $9$ diagonals.
4) The sum of all the interior angles of a regular hexagon is ${720^ \circ }$ and each interior angle is equal to ${120^\circ }$.
5) The sum of all exterior angles of a regular hexagon is ${360^\circ }$ and each exterior angle is equal to ${60^\circ }$.
Assume the length of each side of the design to be a cm as a regular hexagon has an equal number of sides. Now count the number of sides of the design. Then use the formula-
The perimeter of regular hexagon = number of sides × length of the side
Now put the values of perimeter and number of sides in the formula and solve the obtained function to get the answer.
Complete step by step solution:
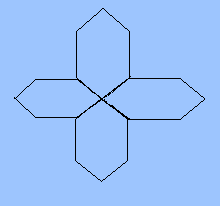
Given, four regular hexagons are drawn as shown below-

The perimeter of the design=$28{\text{ cm}}$
We have to find the length of each side of the hexagon.
A regular hexagon has equal sides and equal angles. So, all the sides of the given design have equal sides. Let the length of one side is a cm.
According to the arrangement of hexagons, the number of sides=$14$
Now we know that perimeter is the sum of all sides of the polygon.
So we can write, the perimeter of given regular hexagon = number of sides × length of the side
On putting the values of perimeter, length, and number of sides we get-
$ \Rightarrow 28 = 14 \times a$
On adjusting, we get-
$ \Rightarrow a = \dfrac{{28}}{{14}}$
On division, we get-
$ \Rightarrow a = 2$
Hence the length of each side of the hexagon is $2{\text{ cm}}$.
Note:
The properties of a regular hexagon are-
1) It has six sides and six angles.
2) All the sides and measures of angles are equal to each other.
3) The regular hexagon has total $9$ diagonals.
4) The sum of all the interior angles of a regular hexagon is ${720^ \circ }$ and each interior angle is equal to ${120^\circ }$.
5) The sum of all exterior angles of a regular hexagon is ${360^\circ }$ and each exterior angle is equal to ${60^\circ }$.
Recently Updated Pages
Master Class 6 Maths: Engaging Questions & Answers for Success

Master Class 6 English: Engaging Questions & Answers for Success

Master Class 6 Science: Engaging Questions & Answers for Success

Class 6 Question and Answer - Your Ultimate Solutions Guide

Master Class 6 Social Science: Engaging Questions & Answers for Success

Master Class 8 Social Science: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples for herbs , shrubs , climbers , creepers

How many millions make a billion class 6 maths CBSE

What is the capital city of Australia? A) Sydney B) Melbourne C) Brisbane D) Canberra

What is the shape of Earth A Circle B Square C Sphere class 6 social science CBSE

The planet nearest to earth is A Mercury B Venus C class 6 social science CBSE

What are the main physical divisions of India class 6 social science CBSE





