Question

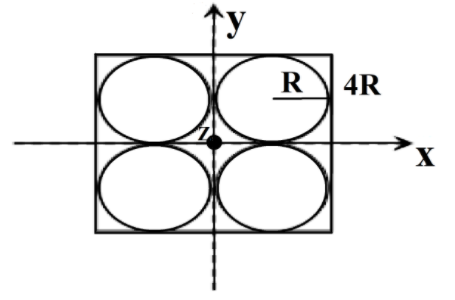
Four holes of radius R are cut from a thin square plate of side 4R and mass M. The moment of inertia of the remaining portion about z-axis is

A. $\dfrac{\pi }{12}M{{R}^{2}}$
B. $(\dfrac{4}{3}-\dfrac{\pi }{4})MR$
C. $(\dfrac{4}{3}-\dfrac{\pi }{4})M{{R}^{2}}$
D. $(\dfrac{8}{3}-\dfrac{10\pi }{16})M{{R}^{2}}$

Answer 1

Hint: While solving this question, go through each shape and part step by step. First find out the moment of inertia of the whole plate and then moment of inertia of one circle. Combined moment of inertia of four circles will be four times the MI of one circle.

Complete answer:
Let us take a look at all the given parameters,
Radius of each circular hole = R
length of side of the square sheet = L = 4R
Now,
Moment of inertia of the whole sheet about z-axis will be
\[~~~{{I}_{z}}={{\dfrac{ML}{6}}^{2}}\]
$\begin{align}
  & \Rightarrow {{I}_{z}}=\dfrac{M{{(4R)}^{2}}}{6} \\
 & \Rightarrow {{I}_{z}}=\dfrac{8M{{R}^{2}}}{3} \\
\end{align}$
Now,
Mass of sheet = M
And, Area of one circle, \[~A=\pi {{R}^{2}}\]
Mass of each circle, ${{m}_{1}}=\dfrac{M}{{{(4R)}^{2}}}\times \pi {{R}^{2}}=\dfrac{\pi M}{16}$
Now,
Moment of inertia of the hole about centre,
 \[\begin{align}
  & \Rightarrow {{I}_{o}}=\dfrac{1}{2}{{m}_{1}}{{R}^{2}} \\
 & \Rightarrow {{I}_{o}}=\dfrac{1}{2}\times \dfrac{\pi M}{16}\times {{R}^{2}} \\
 & \Rightarrow {{I}_{o}}=\dfrac{\pi M{{R}^{2}}}{32} \\
\end{align}\]
So, we have
Moment of inertia of each hole about z axis,
\[{{I}_{1z}}=\dfrac{\pi M{{R}^{2}}}{32}+{{m}_{1}}{{d}^{2}}\]
Where, d = distance between centre of the circle and the centre of the square plate, i.e., \[\sqrt{2}R\]
 \[\begin{align}
  & \Rightarrow {{I}_{1z}}=\dfrac{\pi M{{R}^{2}}}{32}+\dfrac{\pi M}{16}{{(\sqrt{2}R)}^{2}} \\
 & \Rightarrow {{I}_{1z}}=\dfrac{\pi M{{R}^{2}}}{32}+\dfrac{\pi M}{8}{{R}^{2}} \\
 & \Rightarrow {{I}_{1z}}=\dfrac{5\pi }{32}M{{R}^{2}} \\
\end{align}\]
Now, moment of inertia about z- axis due to 4 circles will be,
$\begin{align}
  & \Rightarrow {{I}_{4z}}=4\times {{I}_{1z}} \\
 & \Rightarrow {{I}_{4z}}=\dfrac{10\pi }{16}M{{R}^{2}} \\
\end{align}$
So,
Moment of inertia of the remaining portion about z-axis is
$\begin{align}
  & \Rightarrow I={{I}_{z}}-{{I}_{4z}} \\
 & \Rightarrow I=(\dfrac{8}{3}-\dfrac{10\pi }{16})M{{R}^{2}} \\
\end{align}$

So, the correct answer is option D, $(\dfrac{8}{3}-\dfrac{10\pi }{16})M{{R}^{2}}$ .

Note:
A rigid body's moment of inertia, otherwise known as the mass moment of inertia, angular mass or rotational inertia, is a quantity that specifies the torque necessary for a desired angular acceleration around a rotational axis; analogous to how mass specifies the force required for a desired acceleration, A rigid body's angular mass or rotational inertia is a quantity that specifies the torque provided by a rotational axis for a desired angular acceleration; similar to how mass specifies the force needed for a desired acceleration.