Question

Four charges ${{q}_{A}}=2\mu C$, ${{q}_{B}}=5\mu C$, ${{q}_{C}}=2\mu C$, ${{q}_{D}}=5\mu C$ are located at the corners of a square ABCD of side $10cm$. What is the net electric field at the centre of the square?
(A). $3.6\times {{10}^{6}}N{{C}^{-1}}$ along OC
(B). $9\times {{10}^{6}}N{{C}^{-1}}$ along OB
(C). $3.6\times {{10}^{6}}N{{C}^{-1}}$ along OA
(D). $9\times {{10}^{6}}N{{C}^{-1}}$ along OD
(E). 0

Answer 1

Hint: The electric field due to a charge at a point depends on the magnitude of charge, the distance of the point from the charge and the absolute permeability. The electric field at point O will be the vector sum of all electric fields due to the charges kept at the corners of the sphere.
Formulas used:
$E=\dfrac{q}{4\pi {{\varepsilon }_{0}}r}$

Complete answer:
Electric field at a point is defined as the work done to bring a unit positive charge from infinity to that point.
The electric field between due to a charge at a point is given by-
$E=\dfrac{q}{4\pi {{\varepsilon }_{0}}r}$
Here, $E$ is the force acting between the charges
$q$ is the magnitude of charge on one of the charges
$r$ is the distance between the charges

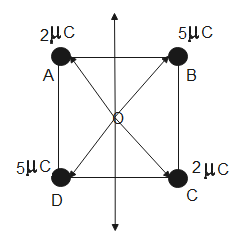
From the above figure, we can see that on each corner of the square a positive charge of different magnitude is kept. Let us assume that a unit positive charge is kept at the center, so the electric field acting on it due to all the positive charges will be repulsive, i.e. away from the charge.

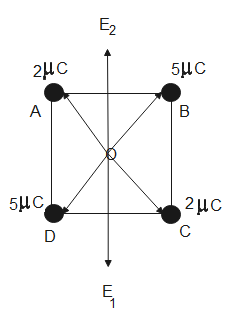
The resultant of electric field due to charge ${{q}_{A}}$ and ${{q}_{B}}$ is ${{E}_{1}}$ and the resultant of force due to charges ${{q}_{C}}$ and ${{q}_{D}}$ is ${{E}_{2}}$.
From the above figure we can see that forces ${{E}_{1}}$ and ${{E}_{2}}$ cancel each other. Thus, the total force acting on the centre is 0.
Therefore, the net electric field acting at the center is 0.

Hence, the correct option is (D).

Note:
Electric field is a vector quantity. Its direction is represented by the electric lines of forces such that the electric lines of forces emerge from the positive charge and end into the negative charge. The direction of electric field is towards the charge for negative charge and away from the charge for positive charge.