Question

What is the formula for the slope of a secant line?

Answer 1

Hint: We will use the equation of slope of a straight line to find the slope of a secant line. We will assume two points of any arbitrary curve, and then find the slope of the line joining these two points. Thus, we will get the slope of the secant line.

Complete step by step solution:
The word secant is derived from a Latin word secare, which means to cut.
We know that a line which intersects the curve at a minimum of two distinct points is called a secant line.
We know that the slope of a line passing through the points $\left( {{x}_{1}},{{y}_{1}} \right)\text{ and }\left( {{x}_{2}},{{y}_{2}} \right)$ is given by
$m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}...\left( i \right)$
Let us now consider an arbitrary function $y=f\left( x \right)$ .

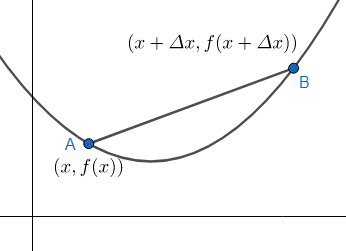
We can clearly see that for this curve, line AB is a secant line.
So, we can write the slope of line AB as,
$m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$
$\Rightarrow m=\dfrac{f\left( x+\Delta x \right)-f\left( x \right)}{\left( x+\Delta x \right)-x}$
Hence, we can easily write
$m=\dfrac{f\left( x+\Delta x \right)-f\left( x \right)}{\Delta x}$
It is very clear from the figure, that this slope is nothing but the average rate of change in f(x).
Thus, we can say that the slope of a secant is the same as the average rate of change.
And this slope is equal to,
$m=\dfrac{f\left( x+\Delta x \right)-f\left( x \right)}{\Delta x}$

Note: We should understand that the line is not a secant until it intersects the curve at least at 2 points. Here, both of the points $\left( {{x}_{1}},{{y}_{1}} \right)\text{ and }\left( {{x}_{2}},{{y}_{2}} \right)$ lies on the curve $y=f\left( x \right)$ . Slope of the secant line is also referred to as the average rate of change of the curve, between 2 points, so we must not get confused by different terms.