Question

Force between the plates of a parallel plate capacitor.

Answer 1

Hint: To solve this problem, first find the electric field by plate which gives a relationship between electric field and area density of charge. But, we know, the area density of charge is the ratio of charge to area. Substitute this equation in the formula for electric field. Then, use the formula for force between two plates which is a product of charge and electric field due to plate. Substitute the value of the electric field and find the value of force. This obtained value is the force between the plates of the parallel plate capacitor.
Formula used:
$E= \dfrac {\sigma}{2 {\epsilon}_{0}}$
$\sigma= \dfrac {Q}{A}$
$F= Q. E$

Complete answer:

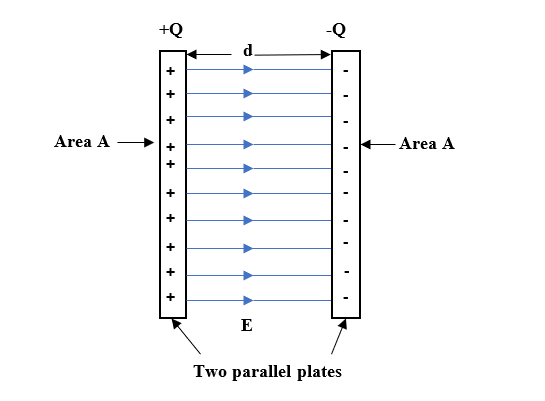
Electric field by any one plate is given by,
$E= \dfrac {\sigma}{2 {\epsilon}_{0}}$ ...(1)
Where, E is the electric field
              $\sigma$ is the area density of charge
             ${\epsilon}_{0}$ is the vacuum permittivity
We know,
Area density of charge is given by,
$\sigma= \dfrac {Q}{A}$ ...(2)
Where, Q is the total charge on the plate
              A is the area of each plate
Substituting equation. (2) in equation. (1) we get,
$E= \dfrac {Q}{2A {\epsilon}_{0}}$ ...(3)
Force between two plates of the capacitor is given by,
$F= Q. E$
Where, F is the force between two plates
Substituting equation. (3) in above equation we get,
$F=Q. \dfrac {Q}{2A {\epsilon}_{0}}$
$\Rightarrow F= \dfrac {{Q}^{2}}{2A {\epsilon}_{0}}$
Hence, the force between the plates of the parallel plate capacitor is $\dfrac {{Q}^{2}}{2A {\epsilon}_{0}}$.

Note:
Amount of charge a capacitor can store depends on two factors. First is the voltage and second is the physical characteristics of the capacitors. The capacitance depends on the dielectric constant of the medium between the plates, area of each plate and distance between the plates. When a dielectric medium is placed between the two parallel plates of the capacitor, it’s capacity of storing the energy increases. Its energy increases by a factor K which is called a dielectric constant. If you want to increase the capacitance of parallel plate capacitors then increase the area, decrease the separation between two plates and use a dielectric medium.