Question

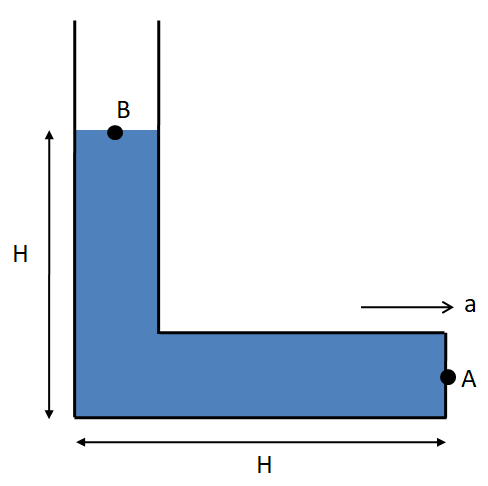
For the L-shaped vessel shown in the figure, determine the value of acceleration $a$ so that the pressure at the point A becomes equal to $\dfrac{{{p_0}}}{2}$? (${p_0}$ is atmospheric pressure)

(A) $g$
(B) $\dfrac{g}{2} + \dfrac{{{p_0}}}{{2\rho h}}$
(C) $\dfrac{{{p_0}}}{{2\rho H}} + g$
(D) $\dfrac{{3{p_0}}}{{2\rho H}} + g$

Answer 1

Hint To solve this question, we need to find out the pressures at the point A and B in terms of the atmospheric pressure. For this, we need to consider the distance of these points in the direction of the two accelerations of the fluid and apply the formula of the pressure in terms of the acceleration.

Formula Used: The formula which is used in solving this question is given by
$\Rightarrow P = {P_o} + \rho ad$, here $P$ is the pressure of the fluid of density $\rho $ at a point which is situated at a distance of $d$ in the direction of the acceleration $a$ of the fluid, from the point where the pressure is equal to ${P_0}$.

Complete step by step answer
From the options given, we see that the density of the fluid contained in the vessel is $\rho $.
Now, as the vessel is accelerated towards right with the acceleration of $a$, the fluid particles will experience a pseudo force in the opposite direction. So the free surface of the fluid will become tilted as shown in the figure below.

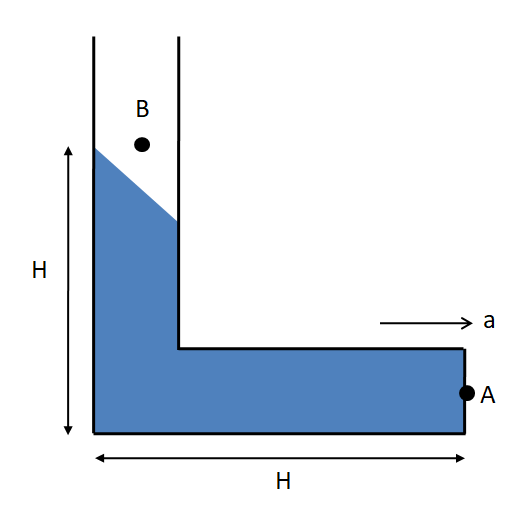
As we can clearly see in the above figure that due to the acceleration of the vessel, there is no fluid particle at the point B. So the pressure at that point becomes equal to the atmospheric pressure. Therefore we have
$\Rightarrow {P_B} = {p_0}$ (1)
We know that the pressure at a point in terms of the acceleration is given by
$\Rightarrow P = {P_o} + \rho ad$ (2)
Now, the point A is at a distance of $H$ in the direction of the acceleration $g$ from the point B.
Also, the point A is at a distance of $H$ from the point B towards the right. But the acceleration of the fluid particles is towards the left (opposite to the acceleration of the vessel). So, the point A is at a distance of $ - H$ from the point B in the direction of the acceleration $a$. So the net pressure at the point A from (2) is
$\Rightarrow {P_A} = {P_B} + \rho gH + \rho a\left( { - H} \right)$
$\Rightarrow {P_A} = {P_B} + \rho gH - \rho aH$
From (1)
$\Rightarrow {P_A} = {p_0} + \rho gH - \rho aH$
$\Rightarrow \rho aH = {p_0} - {P_A} + \rho gH$
According to the question, ${P_A} = \dfrac{{{p_0}}}{2}$. So we have
$\Rightarrow \rho aH = {p_0} - \dfrac{{{p_0}}}{2} + \rho gH$
$\Rightarrow \rho aH = \dfrac{{{p_0}}}{2} + \rho gH$
On dividing both sides by $\rho H$ we get
$\Rightarrow a = \dfrac{{{p_0}}}{{2\rho H}} + g$
This is the required value of the acceleration.
Hence the correct answer is option C.

Note
We should not take the acceleration of the fluid in the direction of acceleration of the vessel. It is the acceleration of the vessel not the fluid which is given in the question. The acceleration of the fluid will be due to the pseudo force which always acts opposite to the acceleration of the vessel.