Question

For function $ f\left( x \right)=x\cos \dfrac{1}{x},x\ge 1, $
(This question has multiple correct options)
A. For at least one x in interval $ \left[ 1,\infty \right],f\left( x+2 \right)-f\left( x \right) < 2 $
B. $ \displaystyle \lim_{x \to \infty }f'\left( x \right)=1 $
C. For all ‘x’ in the interval $ \left[ 1,\infty \right],f\left( x+2 \right)-f\left( x \right) > 2 $
D. $ f\left( x \right) $ is strictly decreasing in the interval $ \left[ 1,\infty \right] $

Answer 1

Hint: We are given that $ f\left( x \right)=x\cos \dfrac{1}{x},x\ge 1, $
We have to check which one of all the options is correct, we differentiate our function then find its limit; we find the 2nd derivative to check the decreasing internal or the function.
We use lap range to check that how the function behaves, how its value is greater or less than 2 or $ x\in \left[ 1,\infty \right] $

Complete step by step answer:
We are given that we have a function $ f\left( x \right)=x\cos \dfrac{1}{x} $ where $ x\ge 1 $
Now we first differentiate it one time
As we have our function as a product of two functions that is x and $ \cos \dfrac{1}{x} $ , we will use the product rule.
 $ d\left( uv \right)=\left( vdu \right)+udv $
So, using this, we get –
 $ f'\left( x \right)=\cos \left( \dfrac{1}{x} \right)\dfrac{d\left( x \right)}{dx}+x\dfrac{d\left( \cos \left( \dfrac{1}{x} \right) \right)}{dx} $
So by simplifying and solving we get –
 $ f'\left( x \right)=\cos \dfrac{1}{x}+\dfrac{1}{x}\sin \dfrac{1}{x} $
Now as $ x \to \infty $
 $ \dfrac{1}{x}\to 0 $
So $ \cos \left( \dfrac{1}{x} \right)\to 1 $ and $ \dfrac{1}{x}\sin \left( \dfrac{1}{x} \right)\to 0 $
So,
 $ \displaystyle \lim_{x \to 0}f'\left( x \right)=\displaystyle \lim_{x \to \infty }\left( \dfrac{1}{x}\sin \dfrac{1}{x}+\cos \dfrac{1}{x} \right) $
 $ =0+1=1 $
So option (B) is Correct.
Now as we have $ x\in \left[ 1,\infty \right] $
So, $ \dfrac{1}{x}\in \left[ 0,1 \right] $
Now if we find double derivate of ‘f’ we get –
 $ f'\left( x \right)=-\dfrac{1}{x}\cos \left( \dfrac{1}{x} \right) $
Now as $ \cos \left( \dfrac{1}{x} \right) $ is positive on $ \left[ 0,1 \right] $ as $ \dfrac{1}{x}\in \left[ 0,1 \right] $ and $ \dfrac{1}{x} $ is also positive.
So we get –
On $ x\in \left[ 1,\infty \right] $
 $ f'\left( x \right)=-\dfrac{1}{{{x}^{3}}}\cos \left( \dfrac{1}{x} \right) $ is negative
So as ‘f’ is strictly decreasing on the internal $ \left[ 1,\infty \right] $
Now, we get earlier that –
 $ f'\left( x \right)=\dfrac{1}{x}\sin \dfrac{1}{x}+\cos \dfrac{1}{x} $
At $ x=1 $ , we have –
 $ f'\left( 1 \right)=\sin 1+\cos 1 $
Which is clearly greater than 1.
 $ \Rightarrow f'\left( 1 \right) > 1 $
As $ \displaystyle \lim_{x \to \infty }f'\left( x \right)=1 $ (solved earlier)
And $ f'\left( x \right) $ is strictly decreasing so, we have that graph of $ f'\left( x \right) $ is given as –

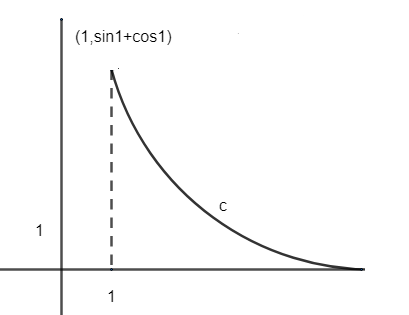
So clearly $ f'\left( x \right) > 1 $ for all $ x\left[ 1,\infty \right] $ ……………………….. (1)
Now, as we can see first $ f'\left( x \right) $ is continuous and differentiable so applying lag rage mean value theorem on $ \left[ x,x+2 \right] $ where $ x\in \left[ 1,\infty \right] $
We have –
 $ f'\left( x \right)=\dfrac{f\left( x+2 \right)-f\left( x \right)}{2} $
As from (1), $ f'\left( x \right) > 1 $
So, $ 1 < \dfrac{f\left( x+2 \right)-f\left( x \right)}{2} $
So we get that –
 $ f\left( x+2 \right)-f\left( x \right) > 2 $ for $ x\in \left[ 1,\infty \right] $
So for all $ x\in \left[ 1,\infty \right]f\left( x+2 \right)-f\left( {} \right) > 2 $
Hence, option (c) is correct.
As option (a) is counter at option (c), and since (c) is correct for all x,
For which $ f\left( x+2 \right)-f\left( x \right) < 2 $ ,
So (A) is incorrect.
So, the correct options are (B), (C) and (D).

Note:
 Remember that it is a function that consists of another function inside it then we have to differentiate it by using a chain method.
 $ d\left[ u\left( v \right) \right]=d\left[ u\left( v \right) \right].d\left( v \right) $ that is first we differentiate first function taking inside function as variable, than we differentiate inside function by taking it as separate function.