Question

For function $f\left( x \right)=\dfrac{{{e}^{x}}+1}{{{e}^{x}}-1}$, if n(d) denotes the number of integers which are not in its domain a n(r) denotes the number of integers which are not in its range, then n(d)+n(r) is equal to:
(a) 2
(b) 3
(c) 4
(d) infinite

Answer 1

Hint: First find the points where function is not defined. Now remove those points. The range of values that you get will be your domain. Now take the function as y, cross multiply the terms and then take an algebraic equation to try to bring all x- terms together. Now find an equation of x in terms of y. Now check where this function of y is not defined. Now remove these points. Now the range of values in your hand at present will be the range of the given function. Now find the number of integers you removed in both domains, range calculations and add them together. The sum you get will be the result.

Complete step-by-step answer:
Domain of a function: In Mathematics, the domain of a function is the set into which all of the input of a function is constrained to fall. It is the set x, in the representation $x\to y$.
Range of function: In mathematics, range of a function is the set into which all the outputs of functions are constrained to fall. It is the set y in the representation $x\to y$.
Given function in the equation as follow here:
$f\left( x \right)=\dfrac{{{e}^{x}}+1}{{{e}^{x}}-1}$
A function is not defined if the denominator is zero. So, we now equate the denominator of fraction to the value zero, we get:
${{e}^{x}}-1=0$
By adding 1 on both sides of the equation, we get it as:
${{e}^{x}}=1$
We know the x satisfying the above is x=0
So, domain of function is given by $R-\left\{ 0 \right\}$
According to question, as we removed 1 integer
$\Rightarrow n\left( d \right)=1.........(i)$
Now equating function to y and cross multiplying, we get:
$y\left( {{e}^{x}}-1 \right)={{e}^{x}}+1$
Subtracting ${{e}^{x}}$ and adding y on both sides, we get:
$y{{e}^{x}}-{{e}^{x}}=y+1$
So, by dividing with y-1 on both sides we get:
${{e}^{x}}=\dfrac{y+1}{y-1}$
We know that ${{e}^{x}}$ is always positive. So, the term $\dfrac{y+1}{y-1}>0$.
The y range satisfying above equation is

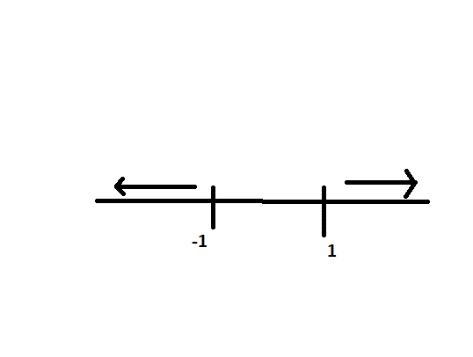
So, range of function $=R-\left[ -1,1 \right]$
So, we removed the range $\left[ -1,1 \right]$ from real numbers to get the range of the function. So, we need the number of integers in $\left[ -1,1 \right]=-1,0,1$.
So, we get 3.
According to question, we get the value of \[n\left( r \right)=3.........(ii)\]
By adding equation (i), (ii), we get
n(d)+n(r)=4
Therefore option (c) is the correct answer.

Note: Generally, students forget to take square brackets. Here -1,1 are included in removed because at -1 the term is zero. By exponential always positive and 1 is removed because at 1 x is not defined. Carefully point out the points and then remove them and count them.