Question

For any two statements $p$ and $q$, the negation of the expression $p \vee \left( { \sim p \wedge q} \right)$ is
A. $p \wedge q$
B. \[p \leftrightarrow q\]
C. $\sim p \vee \sim q$
D. $\sim p \wedge \sim q$

Answer 1

Hint:We will solve this problem using the operations (resembling the set theory relations) on the given expression. Some options in the question may be broken down further into simpler forms using De Morgan’s law. Then, we can reach the correct option out of the four.
We will see another method of solving these types of questions using the Venn diagram concept.

Complete step-by-step answer:
Method-I:
The given expression is $p \vee \left( { \sim p \wedge q} \right)$.
Thus, the negation of this expression can be written as:
$ \sim \left( {p \vee \left( { \sim p \wedge q} \right)} \right)$
$ = \sim p \wedge \sim \left( { \sim p \wedge q} \right)$ $\left[ {\because \sim \left( {a \vee b} \right) \equiv \sim a \wedge \sim b} \right]$
$ = \sim p \wedge \left( {p \vee \sim q} \right)$ $\left[ {\because \sim \left( {a \wedge b} \right) \equiv \sim a \vee \sim b} \right]$
$ = \left( { \sim p \wedge p} \right) \vee \left( { \sim p \wedge \sim q} \right)$ $\left[ {\because c \wedge \left( {a \vee b} \right) \equiv \left( {c \wedge a} \right) \vee \left( {c \wedge b} \right)} \right]$
$ = F \vee \left( { \sim p \wedge \sim q} \right)$ $\left[ {\because \sim a \wedge a \equiv F} \right]$
$ = \left( { \sim p \wedge \sim q} \right)$ $\left[ {\because F \vee a \equiv a} \right]$
Hence option (D) is the correct answer.
Method-II:
Let us draw the Venn diagram for the two compound statements $p$ and $q$.

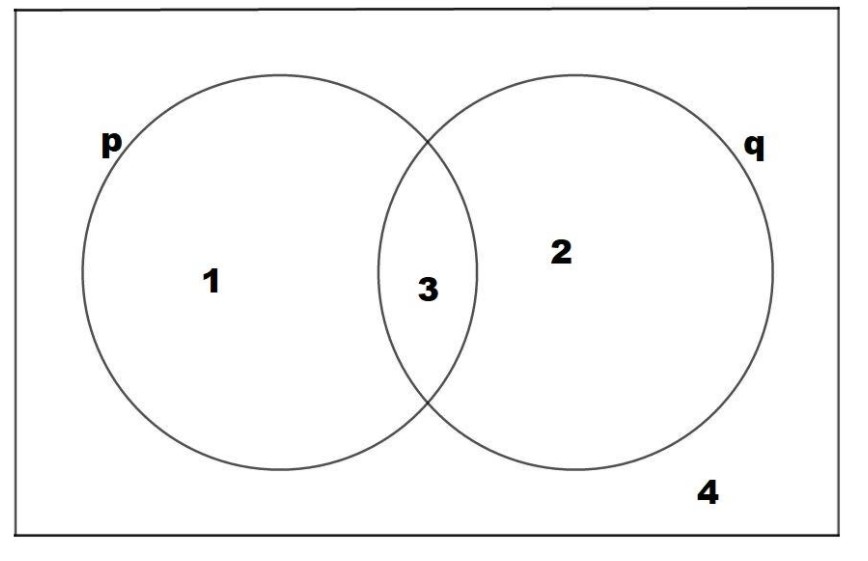
Venn Diagram for two statements p and q
In the Venn diagram,
$p$ has its truth value as $T$ in regions $1$ and $3$.
$q$ has its truth value as $T$ in regions $2$ and $3$.
$ \sim p$ has its truth value as $T$ in regions $2$ and $4$.
$ \sim q$ has its truth value as $T$ in regions $1$ and $4$.
The given expression is $p \vee \left( { \sim p \wedge q} \right)$.

Thus, the negation of this expression can be written as $ \sim \left( {p \vee \left( { \sim p \wedge q} \right)} \right)$. We will solve this expression to find region(s) in the Venn diagram in the following steps:
1) $ \sim p \wedge q$ has its truth value as $T$ in region(s) common to regions of $ \sim p$ and $q$.
2) The common region is region $2$ by observation. Thus, $ \sim p \wedge q$ has its truth value as $T$ in region $2$.
3) Now, $p \vee \left( { \sim p \wedge q} \right)$ has its truth value as $T$ in $p \vee region2$, i.e., regions $1,2,3$.
4) The last step is to find the region of Truth Values of $ \sim \left( {p \vee \left( { \sim p \wedge q} \right)} \right)$as $T$. $ \sim \left( {p \vee \left( { \sim p \wedge q} \right)} \right)$ comes by taking negation of ($p \vee region2$). i.e., region $4$.

Let us consider the options now. The one that has region 4 as the $T$ value is the required answer:
A. $p \wedge q$ has Truth value as $T$ in region(s) $2$ [By observing the Venn Diagram]
B. \[p \leftrightarrow q\] has Truth value as $T$ in region(s) $3,4$ [when both $F$ or both $T$]
C. $ \sim p \vee \sim q$ has Truth value as $T$ in region(s) $1,2,4$ [By observing the Venn Diagram]
D. $ \sim p \wedge \sim q$ has Truth value as $T$ in region(s) $4$ [By observing the Venn Diagram]
Hence, $ \sim \left( {p \vee \left( { \sim p \wedge q} \right)} \right) = \sim p \wedge \sim q$

So, the correct answer is “Option D”.

Note:Sometime it takes a quite long time if we want to solve these kinds of problems by the Venn diagram method subjectively. We have to keep our mind open as to when to use the Venn diagram method. When it is an objective problem, it is recommended to use the ${2^{nd}}$method. Also, in case or three statements [e.g., \[q \leftrightarrow \left( {p \wedge \sim r} \right)\]], it is highly recommended to use the Venn diagram method.