Question

For any real number x, define [x] = greatest integer less than or equal to x. Prove that the greatest integer function $f:R\to R:f\left( x \right)=\left[ x \right]$ is neither one-one nor onto.

Answer 1

Hint:First of all check the different images of the given function. If they are the same for different x. Then the function is not one-one. Now, check the range and domain of the function. If they are not the same, then the function is not onto.

Complete step-by-step answer:
In this question, we are given that [x] = greatest integer less than or equal to x. We have to prove that the function $f:R\to R:f\left( x \right)=\left[ x \right]$ is neither one-one nor onto.
Let us consider our question, we are given that, $f:R\to R:f\left( x \right)=\left[ x \right]$. Let us draw the graph for $f\left( x \right)=\left[ x \right]$.

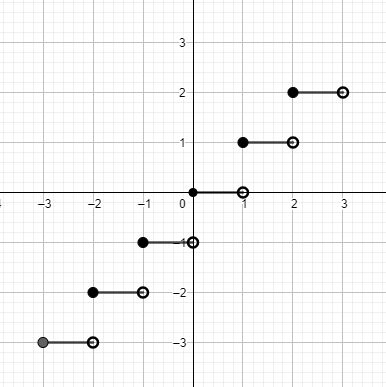
From the above figure, we can see that,
For $x\in \left[ 0,1 \right),f\left( x \right)=0$
For $x\in \left[ 1,2 \right),f\left( x \right)=1$
For $x\in \left[ -1,0 \right),f\left( x \right)=-1$ and so on.
So, for example, at some x, we get the values as follows:
[1] = 1
[1.2] = 1
[1.9] = 1
[2] = 2 and so on.
Now, let us check if this function is one-one or not.
We know that for a function to be one-one, it’s different elements must have different images or we can say that $f\left( {{x}_{1}} \right)=f\left( {{x}_{2}} \right)\leftrightarrow {{x}_{1}}={{x}_{2}}$ or ${{x}_{1}}\ne {{x}_{2}}\leftrightarrow f\left( {{x}_{1}} \right)\ne f\left( {{x}_{2}} \right)$. But in this function, for different values of x, y are the same. For example, f (1) = 1, f (1.2) = 1, f (1.9) = 1, f (1.99) = 1. So, different elements 1.2, 1.9, 1.99, etc. have the same image 1. So, this function is not one-one.
Now, let us check if this function is onto or not.
We know that, for a function to be onto, the range of the function must be equal to its domain. $f:R\to R:f\left( x \right)=\left[ x \right]$
If $f:A\to B$, then B is the co-domain of function. In the given function, co-domain is given as R that is all rational numbers. But from the graph of $f\left( x \right)=\left[ x \right]$, we can clearly see that $f\left( x \right)=\left[ x \right]$ only takes integral values or it’s range is only integers. So, for $f\left( x \right)=\left[ x \right]$, the range is not equal to co-domain. So, this function is not onto.
Hence, we have proved that this function is neither one-one nor onto function.

Note: Students can also check if a function is one-one or not by drawing a line parallel to x-axis in the graph of f (x). If the line intersects the function at just one point then function, f (x) is one-one, else not. Also, whether a function is onto or not depends on the given co-domain. So, according to the given co-domain, a function may or may not be onto.