Question

How do I find the x intercept of a quadratic function in vertex form $f\left( x \right)=\dfrac{1}{4}{{\left( x+2 \right)}^{2}}-9$ ?

Answer 1

Hint: The x intercept of any function is the points where the curve of function cuts the x axis that means the value of function is 0 at x intercept. So actually the roots of the equation are x intercepts of the equation.

Complete step by step answer:
The given vertex form of the quadratic equation is $\dfrac{1}{4}{{\left( x+2 \right)}^{2}}-9$
The coordinate of vertex is (-2,-9)
We have to find the x intercepts of the equation
We know that the x intercepts are roots of the equation, where the value of the function is 0
So now we have to solve $\dfrac{1}{4}{{\left( x+2 \right)}^{2}}-9=0$
So there are maximum 2 x intercepts possible for $\dfrac{1}{4}{{\left( x+2 \right)}^{2}}-9$
Adding 9 in both LHS and RHS
$\dfrac{1}{4}{{\left( x+2 \right)}^{2}}=9$
Multiplying 4 in both LHS and RHS we get
${{\left( x+2 \right)}^{2}}=36$
So now we can see $\left( x+2 \right)=\pm \sqrt{36}$
The value $x+2$ can be 6 0r -6
So the value of x can be 4 or -8
So the x intercepts of $\dfrac{1}{4}{{\left( x+2 \right)}^{2}}-9$ are 4 and -8.
$\dfrac{1}{4}{{\left( x+2 \right)}^{2}}-9$ intersect x axis at point (4,0) and (-8,0)
We can draw the graph of $\dfrac{1}{4}{{\left( x+2 \right)}^{2}}-9$

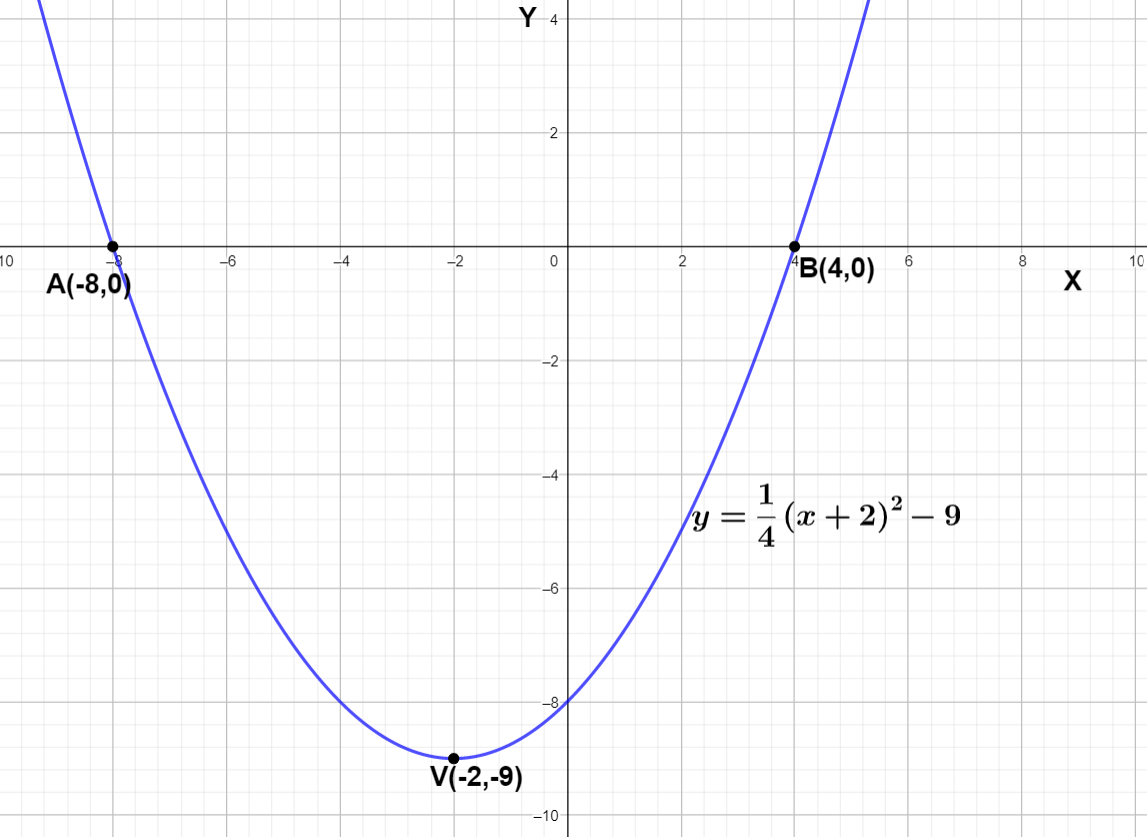
We can see the vertex is point V(-2,-9) and the 2 x intercepts are A(-8,0) and B(4,0).

Note:
If the 2 function f and g are inverse function of each other, then the x intercept of f is equal to y intercept of g. The y intercept of f is equal to x intercept of g this is because the function f and g are mirror images of each other with respect to the straight line $y=x$ .