Question

Find the volume of the cylinder in which height = 42cm and base radius =10cm.

Answer 1

Hint: We have to find the volume of the cylinder, using formula directly, the volume of a cylinder(V) having radius as R and height of cylinder as H will be \[V=\pi {{R}^{2}}H\] We know the values of R and H so on putting the values we will get the desired volume of the cylinder.

Complete step-by-step solution:

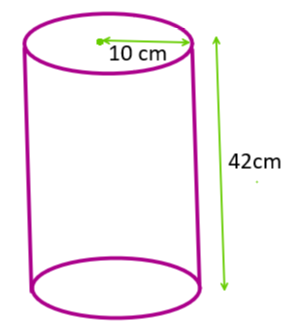
Given a cylinder which having a base radius as 10cm and height of cylinder is given as 42 cm and we have to find the volume of that cylinder. Actually the meaning of volume is the total space inside that object so it will be calculated by multiplying height with uniform cross section area so here the height will be H(42cm) and uniform cross section area will be \[\pi {{R}^{2}}\] so on multiplying both we get our volume will be \[V=\pi {{R}^{2}}H\]now on substituting value \[R=10cm\] and \[H=42cm\] we get volume expression as \[V=\pi \times {{(10)}^{2}}\times (42)\] approx the value of \[\pi \] to be 3.14 so on solving we get Volume equals to \[V=3.14\times {{(10)}^{2}}\times (42)\] further solving gives value of volume to be \[13188c{{m}^{3}}\] now here the volume is in \[c{{m}^{3}}\] so to convert this in \[{{m}^{3}}\] divide it by \[{{10}^{6}}\] , so we get value of volume to be \[0.013188{{m}^{3}}\].
Hence the volume of cylinder will be \[0.013188{{m}^{3}}\]

Note: If we are asked to find the total surface area of this cylinder then its formula will be \[TSA=2\pi RH\], here we just want the curved area of the cylinder so we multiply circumference \[2\pi R\]
With the height of cylinder H, so on putting values in formula \[TSA=2\pi RH\], we get expression as
\[TSA=2\pi (10)(42)\] which on solving gives \[TSA=2637.6c{{m}^{2}}\]or dividing it by \[{{10}^{4}}\] we got TSA in
Terms of \[{{m}^{2}}\] as \[TSA=0.26376{{m}^{2}}\]