Question

How do you find the vertex of $y=-2\left( x+3 \right)\left( x-1 \right)$?

Answer 1

Hint: In this question we have been given with an equation of a parabola which is in the factored form. We will use the property of the vertex that the vertex lies on the axis of symmetry of the parabola which is the midpoint value of the zeros. We will find the ${{x}_{vertex}}$ by the midpoint value and then substitute it in the given equation and simplify to get the value of the ${{y}_{vertex}}$ and then write the coordinate of the vertex which will be $\left( {{x}_{vertex}},{{y}_{vertex}} \right)$.

Complete step by step solution:
We have the equation given to us as:
$\Rightarrow y=-2\left( x+3 \right)\left( x-1 \right)$
Now to find the zeros of the expression, we will substitute $y=0$ and solve for the value of $x$.
On substituting, we get:
$\Rightarrow 0=-2\left( x+3 \right)\left( x-1 \right)$
On simplifying, we get:
$\Rightarrow 0=\left( x+3 \right)\left( x-1 \right)$
Therefore, we get:
$x+3=0$ and $x-1=0$
On rearranging the equations, we get:
$x=-3$ and $x=1$
Now the value of the ${{x}_{vertex}}$ is the midpoint of the zeros therefore, we get:
$\Rightarrow {{x}_{vertex}}=\dfrac{-3+1}{2}$
On simplifying, we get:
$\Rightarrow {{x}_{vertex}}=-1$
Now substituting $x=-1$ in the equation, we get:
$\Rightarrow {{y}_{vertex}}=-2\left( -1+3 \right)\left( -1-1 \right)$
On simplifying the brackets, we get:
$\Rightarrow {{y}_{vertex}}=-2\left( 2 \right)\left( -2 \right)$
On multiplying the terms, we get:
$\Rightarrow {{y}_{vertex}}=8$
Therefore, the coordinates of the vertex are $\left( -1,8 \right)$, which is the required solution.
On drawing it on the graph, we get:

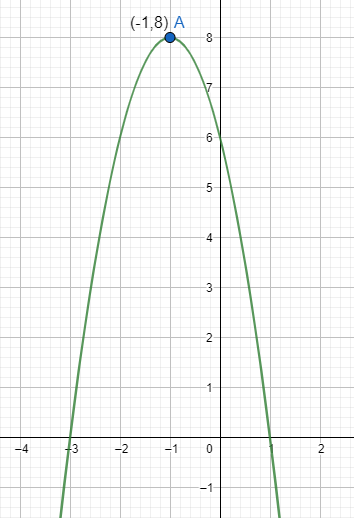
Note: In this question we had the given equation of the parabola in the factorized format. A parabola is in the form of a quadratic equation which is $a{{x}^{2}}+bx+c$. The value of the ${{x}_{vertex}}$ can be found using the formula ${{x}_{vertex}}=\dfrac{-b}{2a}$ and then substituting its value in the equation to get the ${{y}_{vertex}}$ and writing the coordinates of the vertex.