
How do you find the vertex of this parabola \[y=4x-{{x}^{2}}\] ?
Answer
546k+ views
Hint: The above given problem is a very simple problem of coordinate geometry. The sub-topic is parabola, and for solving these types of problems we need to first understand what the different forms of parabolas are possible. There are four general types of parabola and for each of them, the corresponding vertex and foci are as follows,
Complete step by step answer:
Now, starting off with the solution of our given problem, we can first of all rearrange the terms of the given equation to make it look like one of the standardized forms as mentioned in the above table. So rearranging all the terms we get,
\[4x-{{x}^{2}}=y\]
Now, taking the negative sign common in the left hand side we can write,
\[{{x}^{2}}-4x=-y\]
We now add \[4\] on both the left and right hand side of the equation, so that the left hand side becomes a perfect square,
\[{{x}^{2}}-4x+4=-y+4\]
Now writing the L.H.S as a perfect square, we get,
\[{{\left( x-2 \right)}^{2}}=-y+4\]
Now, taking the negative sign common in the right hand side we get,
\[{{\left( x-2 \right)}^{2}}=-\left( y-4 \right)\]
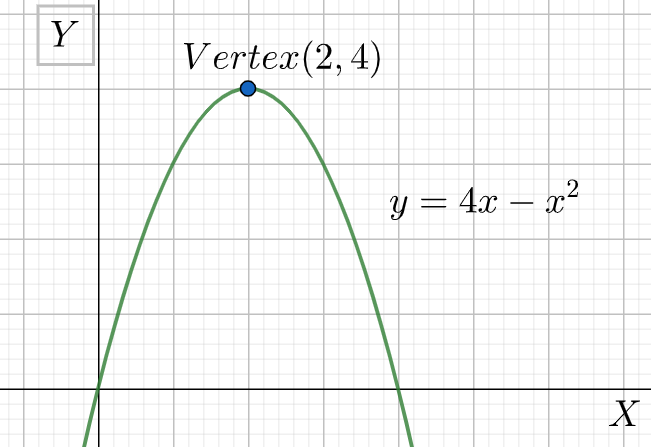
Now, if we take a closer look at the table we discussed below, our rearranged parabolic equation looks something like the last equation, where \[b=\dfrac{1}{4}\] .
We can however rewrite the last parabolic equation as,
\[{{\left( x-0 \right)}^{2}}=-4b\left( y-0 \right)\] and from this it is very clear why for this equation \[\left( 0,0 \right)\] is the vertex. Comparing this equation with the generalized one, we can say that for our given problem \[\left( 2,4 \right)\]is the vertex of the parabola.
Note:
We can also find the vertex using the method of shifting of origin or origin transformation, but it is a very complex as well as a lengthy process. The solution shown above is the simplest one. In origin transformation, we shift the origin of the actual coordinate system, to some other arbitrary system, so as to simplify the equation and make it similar to that of the general form. However to find the required point, we need to revert back to the original coordinate system.
| Equation | Vertex | Foci |
| \[{{y}^{2}}=4ax\] | \[\left( 0,0 \right)\] | \[\left( a,0 \right)\] |
| \[{{y}^{2}}=-4ax\] | \[\left( 0,0 \right)\] | \[\left( -a,0 \right)\] |
| \[{{x}^{2}}=4by\] | \[\left( 0,0 \right)\] | \[\left( 0,b \right)\] |
| \[{{x}^{2}}=-4by\] | \[\left( 0,0 \right)\] | \[\left( 0,-b \right)\] |
Complete step by step answer:
Now, starting off with the solution of our given problem, we can first of all rearrange the terms of the given equation to make it look like one of the standardized forms as mentioned in the above table. So rearranging all the terms we get,
\[4x-{{x}^{2}}=y\]
Now, taking the negative sign common in the left hand side we can write,
\[{{x}^{2}}-4x=-y\]
We now add \[4\] on both the left and right hand side of the equation, so that the left hand side becomes a perfect square,
\[{{x}^{2}}-4x+4=-y+4\]
Now writing the L.H.S as a perfect square, we get,
\[{{\left( x-2 \right)}^{2}}=-y+4\]
Now, taking the negative sign common in the right hand side we get,
\[{{\left( x-2 \right)}^{2}}=-\left( y-4 \right)\]

Now, if we take a closer look at the table we discussed below, our rearranged parabolic equation looks something like the last equation, where \[b=\dfrac{1}{4}\] .
We can however rewrite the last parabolic equation as,
\[{{\left( x-0 \right)}^{2}}=-4b\left( y-0 \right)\] and from this it is very clear why for this equation \[\left( 0,0 \right)\] is the vertex. Comparing this equation with the generalized one, we can say that for our given problem \[\left( 2,4 \right)\]is the vertex of the parabola.
Note:
We can also find the vertex using the method of shifting of origin or origin transformation, but it is a very complex as well as a lengthy process. The solution shown above is the simplest one. In origin transformation, we shift the origin of the actual coordinate system, to some other arbitrary system, so as to simplify the equation and make it similar to that of the general form. However to find the required point, we need to revert back to the original coordinate system.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Class 11 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




