Question

How do you find the vertex and intercepts for $y = 4{x^2} + 8x + 7$ ?

Answer 1

Hint: The equation here represents a parabola. To find the intercepts i.e. the points on the coordinate axes where the curve intersects the coordinate axes, we can assume one of the variables as $\;0$ , and find the value of the other variable. To find the vertex of a parabola, we convert the equation into standard form $y = a{(x - h)^2} + k$ , where $(h,k)$ is the vertex of the parabola.

Complete step-by-step answer:
The equation given here represents a parabola that does not pass through the origin.
The standard form of an equation of a parabola is $y = a{x^2} + bx + c$ .
Comparing the standard equation with the given equation, we get the values
$\Rightarrow$ $a = 4$ , $b = 8$ , $c = 7$
Here $a > 0$ , which means the parabola opens upwards.
Now, to find the intercepts on coordinate axes, we have to assume one of the variables as $\;0$ and find the value of the other variable for it.
Hence, for the Y-intercept, we have to assume $x = 0$
Substituting $x = 0$ in the equation of the parabola given here,
$ \Rightarrow y = 4{(0)^2} + 8(0) + 7$
$ \Rightarrow y = 0 + 0 + 7$
Hence, the final value of the variable $y$ is,
$ \Rightarrow y = 7$
Thus, the Y-intercept of the parabola is $y = 7$or in the Cartesian coordinates $(0,7)$ .
For the X-intercept, we have to assume $y = 0$
Substituting $y = 0$ in the equation of the parabola given here,
$ \Rightarrow 0 = 4{x^2} + 8x + 7$
To make the equation a perfect square, we need to find the last term by the formula
$\Rightarrow$L. T. = $\dfrac{{{b^2}}}{{4a}}$
Substituting the values, we get
$\Rightarrow$L. T. = $\dfrac{{{{(8)}^2}}}{{4(4)}} = \dfrac{{64}}{{16}} = 4$
Hence, adding and subtracting $\;4$ in the equation,
 $ \Rightarrow 0 = 4{x^2} + 8x + 7 + 4 - 4$
Rearranging the terms,
$ \Rightarrow 0 = 4{x^2} + 8x + 4 + 7 - 4$
Taking $\;4$ out as a common factor from the first three terms,
$ \Rightarrow 0 = 4({x^2} + 2x + 1) + 3$
$ \Rightarrow 0 = 4{(x + 1)^2} + 3$
Subtracting $\;3$ on both sides of the equation
$ \Rightarrow - 3 = 4{(x + 1)^2}$
But, we know that the value of a perfect square is always positive
Hence, the parabola does not have an X-intercept
Now, for the vertex of the parabola, convert the equation into the vertex form $y = a{(x - h)^2} + k$
$ \Rightarrow y = 4{(x + 1)^2} + 3$ , where $a = 4$ , $h = - 1$ , $k = 3$
Now, we know that the vertex of a parabola is given as $(h,k)$
Hence, the vertex of the parabola is $( - 1,3)$ .
If we plot the parabola, we get the graph as shown

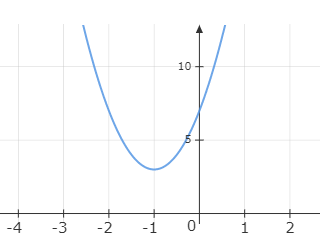
Note:
Here, to find the vertex, we can also use the standard form of the equation $y = a{x^2} + bx + c$ , where the axis of symmetry or the x coordinate is given as $x = \dfrac{{ - b}}{{2a}}$ and then find the value of $y$ from the equation of the parabola.