Question

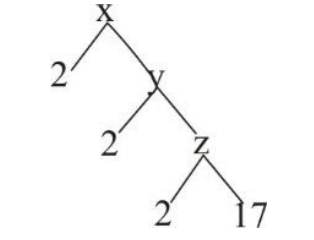
Find the values of x, y and z in the following factor tree. Find the value of x.

Answer 1

Hint: Values of x, y and z can be obtained by using the reverse process of factor tree. Here, the reverse process implies that on multiplying factors together a number is obtained as a result. So, at each step on multiplying factors we get respective number.

Complete step-by-step answer:
In a prime factor tree we know that at each step of the tree prime factors of given number separate out. We keep going through this process until all prime factors of given numbers are obtained.
Hence, in its reverse process of multiplying all prime factors we can obtain the same number whose prime factors are obtained earlier.
Therefore, we use the reverse process to get the value of x, y and z in the given factor tree.
In a given factor tree we start from the bottom and go in an upward direction. Hence, we first get the value of z and then y and finally the value of x.
From the factor tree we see that the factors of z are $ 2\,\,and\,\,17 $ . Hence multiplying $ 2\,\,and\,\,17 $ together results in the value of z.
Therefore, the value of z is $ 34 $ .
Now, at the second step from bottom we see that the factors of y are $ 2\,\,and\,\,z $ .
Hence, on multiplying $ 2\,\,and\,\,z $ we get the value of y.
Therefore, value of y = $ 2 \times z $ , substituting value of z obtained in above step.
  $
  y = 2 \times 34 \\
   \Rightarrow y = 68 \\
  $
Hence, the value of y is $ 68 $ .

Now, at the third step from bottom we see that the factors of x are $ 2\,\,and\,\,y $ .
Therefore, the value of x can be obtained by multiplying $ 2\,\,and\,\,y\,\, $ together.
x = $ 2\,\, \times y $
Substituting value of y to get value of x.
 $
   \Rightarrow x = 2 \times 68 \\
   \Rightarrow x = 136 \\
  $
Hence, the value of x is $ 136 $ .
Therefore, from above we see that the required values of x, y and z are $ 136,\,\,68\,\,and\,\,34 $ respectively.

Note: Any number can be expressed as a product of prime factors by using a prime factor tree. In this process at each step a given number breaks down as a product of two numbers in which one number is prime and another is composite. We repeat the same process on composite numbers and obtain its two factors : one is prime and other is composite. We keep on repeating the same process every time on a composite number till we end with both prime factors.
So, on applying reverse steps from bottom to top on multiplying factors we obtained the respective number with which we started the process.