Question

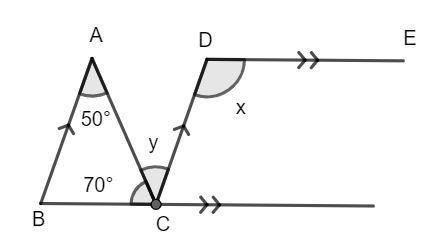
Find the values of x and y from the following figure.

Answer 1

Hint: Recall the properties of parallel lines and angles subtended by an intersecting line. The corresponding angles are equal and the adjacent angles add to 180°. Use this to find the values of the angles x and y.

Complete step-by-step answer:
Two lines are said to be parallel if they never meet at any finite point in space. They are always the same distance apart.
When another line intersects two parallel lines the angles formed as a result have special properties.
The alternate angles are angles formed on the opposite sides of the intersecting lines and they are equal to each other.
The corresponding angles are angles formed on the same side of the intersecting line and they are equal to each other.
The interior angles on the same side of the transversal are supplementary, that is, the sum of their angle is equal to 180°.

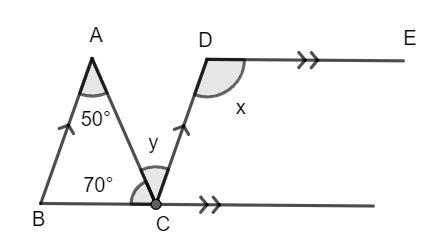
The lines AB and CD are parallel. The angle BAC and angle ACD are alternating angles and hence, they are equal to each other. Then, we have:
\[\angle BAC = \angle ACD\]
\[y = 50^\circ ...........(1)\]
Now, we have the lines BC and DE which are also parallel. The angle BCD and the angle CDE are exterior alternate angles and hence, they are equal. Then, we have:
\[\angle BCD = \angle CDE\]
\[70^\circ + y = x\]
Now, using equation (1), we have:
\[70^\circ + 50^\circ = x\]
Solving for x, we have:
\[x = 120^\circ \]
Hence, the value of x and y are 120° and 50° respectively.

Note: You can also use interior angles properties to find the value of the angle x by finding the angle ABC using the properties of the triangle first and then evaluating.