Question

Find the values of the other five trigonometric functions in $\cot \theta =\dfrac{12}{5},\,\theta $ in quadrant III.

Answer 1

Hint: Sine, cosine, secant, cosec is negative in IIIrd quadrant and cot, tan give positive values in IIIrd quadrant$\left( \text{ }\!\!\pi\!\!\text{ }\,\text{ to }\,\dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{2}} \right)$. Draw a right-angled triangle with the help of a given expression in the problem. I.e. $\cot \theta =\dfrac{12}{5},\,\,\cot \theta $ is defined as$\cot \theta =\dfrac{\text{base}}{\text{perpendicular}}$. Apply Pythagoras rule of the right angle with the help of relation: -

${{\left( \text{hypotenuse} \right)}^{\text{2}}}\text{=}{{\left( \text{base} \right)}^{\text{2}}}\text{+}{{\left( \text{perpendicular} \right)}^{\text{2}}}$
$\text{sin }\!\!\theta\!\!\text{ =}\dfrac{\text{perpendicular}}{\text{hypotenuse}}\text{,}\,\text{tan }\!\!\theta\!\!\text{ =}\dfrac{\text{perpendicualr}}{\text{base}}$ .

And $\sec \theta ,\,\csc \theta ,\,\cot \theta $ are just opposite to $\cos \theta ,\,\sin \theta ,\,\tan \theta $respectively. Use the above identities to evaluate the values of other five functions.

Complete step-by-step answer:

Here, we are given the value of $\cot \theta =\dfrac{12}{5}$, and hence, we need to determine other trigonometric functions, where $\text{ }\!\!\theta\!\!\text{ }$ is lying in IIIrd quadrant.

As, we know the identity for $\cot \theta $ can be given as:

$\cot \theta =\dfrac{\text{base}}{\text{perpendicular}}.........\text{(i)}$

We know

\[\cot \theta =\dfrac{12}{5}...............(ii)\]

It means we can draw a right-angle triangle with one angle as $\text{ }\!\!\theta\!\!\text{ }$ (except $90{}^\circ $) and put the base as 12 units and corresponding perpendicular length as 5 units. So, we can draw a right-angle triangle as per the equation (i) and equation (ii) as

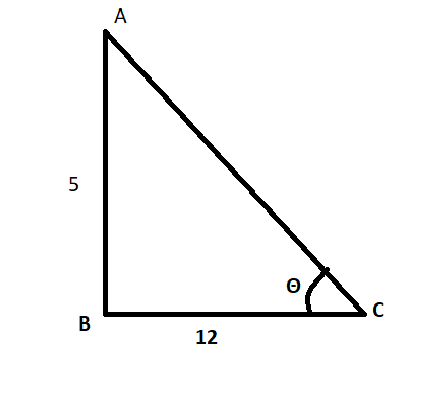
Now, we know that the Pythagoras theorem relation in a right-angle triangle can be given as
\[{{\left( \text{hypotenuse} \right)}^{\text{2}}}\text{=}{{\left( \text{base} \right)}^{\text{2}}}\text{+}{{\left( \text{perpendicular} \right)}^{\text{2}}}..........\text{(iii)}\]

Now, we can get the equation (iii) by using the given triangle ABC as

So, we get,

$\begin{align}

  & {{\left( \text{AC} \right)}^{\text{2}}}\text{=}{{\left( \text{AB}
\right)}^{\text{2}}}\text{+}{{\left( \text{BC} \right)}^{\text{2}}} \\

 & {{\left( \text{AC} \right)}^{\text{2}}}\text{=}{{\left( \text{5}
\right)}^{\text{2}}}\text{+}{{\left( \text{12} \right)}^{\text{2}}} \\

 & {{\left( \text{AC} \right)}^{\text{2}}}\text{=25+144} \\

 & {{\left( \text{AC} \right)}^{\text{2}}}\text{=169} \\

\end{align}$

Taking square root to both the sides we get,

$\begin{align}

  & AC=\sqrt{169} \\

 & AC=13\text{units} \\

\end{align}$

Now, we know value of $\cot \theta =\dfrac{12}{5}$ and we have a triangle ABC that is defined according to the given function in the problem. Let us relate other trigonometric functions with the help of property or rules of quadrants defined for trigonometric functions.

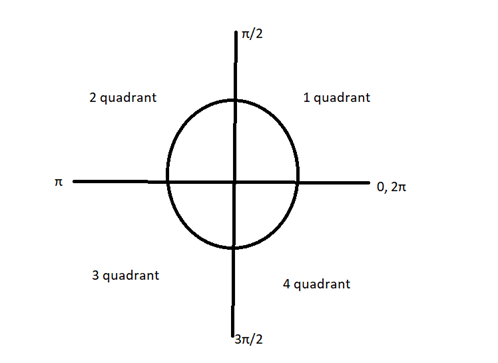
So, as per the given statement in the problem $\theta $ is lying in the IIIrd quadrant, where tan and cot are positive only and others will give negative value only.

So, let us observe the triangle ABC and rules of quadrant for writing values of trigonometric functions.

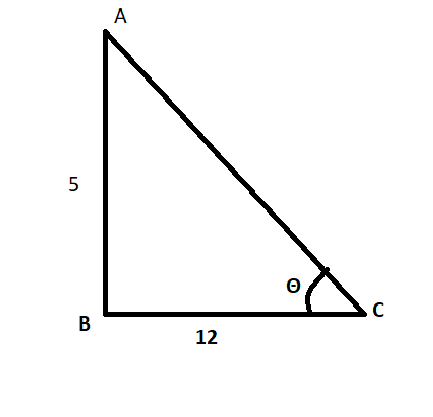
(i) $\sin \theta $

As we know

$\sin \theta =\dfrac{\text{perpendicular}}{\text{base}}.............\text{(iv)}$

As, we know sin function is negative in 3rd quadrant. So, using$\Delta \text{ABC}$, we can write value of $\sin \theta $ as \[\dfrac{5}{13}\] from the equation (iv) but need to put negative sign as the angle belongs to 3rd quadrant.

Hence, we get

$\sin \theta =-\dfrac{5}{13}$

(ii) $\cos \theta $

Similarly, as we know cosine is also negative in 3rd quadrant. So,

\[\cos \theta \text{=}\dfrac{\text{base}}{\text{hypotenuse}}.............\text{(v)}\]

From $\Delta \text{ABC}$, we get

$\cos \theta =\left( \dfrac{12}{13} \right)$

(iii) \[\tan \theta \]

\[\tan \theta =\dfrac{\text{perpendicular}}{\text{base}}\]

Tan is positive in 3rd quadrant. So, we get \[\tan \theta =\dfrac{5}{12}\]

(iv) \[\sec \theta \]

\[\sec \theta =\dfrac{\text{hypotenuse}}{\text{base}}\]

Secant is negative in 3rd quadrant. So, we get \[\sec \theta =-\dfrac{13}{12}\]

(v) \[\csc \theta \]

\[\csc \theta =\dfrac{\text{hypotenuse}}{\text{perpendicular}}\]

Cosecant is also negative in 3rd quadrant. So, we get $\csc \theta =-\dfrac{13}{5}$

Hence, the values of all the trigonometric functions are given as

$\begin{align}

  & \sin \theta =-\dfrac{5}{13} \\

 & \cos \theta =-\dfrac{12}{13} \\

 & \tan \theta =\dfrac{5}{12} \\

 & \cot \theta =\dfrac{12}{5} \\

 & \csc \theta =-\dfrac{13}{3} \\

 & \sec \theta =-\dfrac{13}{12} \\

\end{align}$

Note: One may use the following identities to get other functions as well: -

$\begin{align}

  & {{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1 \\

 & 1+{{\tan }^{2}}\theta ={{\sec }^{2}}\theta \\

 & 1+{{\cot }^{2}}\theta ={{\csc }^{2}}\theta \\

 & \sin \theta =\dfrac{1}{\csc \theta } \\

 & \cos \theta =\dfrac{1}{\sec \theta } \\

 & \cot \theta =\dfrac{1}{\tan \theta }=\dfrac{\cos \theta }{\sin \theta } \\

 & \tan \theta =\dfrac{\sin \theta }{\cos \theta } \\

\end{align}$

But need to take care of quadrant rules for the trigonometric function with the above identities as well. We can eliminate making a right-angle triangle step only with this approach. Be clear with the identities of trigonometric functions and the signs of them in quadrants should be known, students do mistakes with these parts generally. So, always take care and be careful with these kinds of questions.
Remember all the basic fundamental identities of all the trigonometric functions related to right-angled triangle. One may get confuse with all the relations of,$\sec \theta ,\,\csc \theta ,\,\cot \theta $in terms of hypotenuse, base, perpendicular. So, be clear with these relations for solving these kinds of questions.