
Find the value of x and y using cross multiplication method:
\[2x+y=13\] and \[x+y=8\].
A. (5, 3)
B. (5, -3)
C. (-5, -3)
D. (-5, 3)
Answer
603.9k+ views
Hint:Consider two linear equations applying the cross product where the coefficient of x, y and constant terms in the equation are interrelated. Take this relation into formula.
Complete step-by-step answer:
We have been given two equations \[2x+y=13.....(1)\]
\[x+y=8....(2)\]
Now let us look into the formula for cross multiplication and its use in solving two simultaneous equations can be presented as,
\[\begin{align}
& {{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}=0......(3) \\
& {{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}=0.....(4) \\
\end{align}\]
Thus we can draw it as,
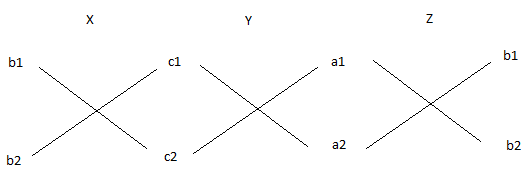
Here z=1
Thus from this we can write as,
\[\dfrac{x}{{{b}_{1}}{{c}_{2}}-{{b}_{2}}{{c}_{1}}}=\dfrac{y}{{{c}_{1}}{{a}_{2}}-{{c}_{2}}{{a}_{1}}}=\dfrac{1}{{{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}}}\]
From this we can write,
\[\begin{align}
& \dfrac{x}{{{b}_{1}}{{c}_{2}}-{{b}_{2}}{{c}_{1}}}=\dfrac{1}{{{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}}} \\
& \Rightarrow x=\dfrac{{{b}_{1}}{{c}_{2}}-{{b}_{2}}{{c}_{1}}}{{{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}}}.....(5) \\
\end{align}\]
\[\begin{align}
& \dfrac{y}{{{c}_{1}}{{a}_{2}}-{{c}_{2}}{{a}_{1}}}=\dfrac{1}{{{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}}} \\
& \therefore y=\dfrac{{{c}_{1}}{{a}_{2}}-{{c}_{2}}{{a}_{1}}}{{{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}}}....(6) \\
\end{align}\]
Thus from equation (1) , \[2x+y-13=0\], compare it with equation (3).
\[{{a}_{1}}=2,{{b}_{1}}=1,{{c}_{1}}=-13\]
Now from equation (2), \[x+y=8\], compare it with equation (4).
\[{{a}_{2}}=1,{{b}_{2}}=1,{{c}_{2}}=-8\]
Now apply these values in equation (5) and (6).
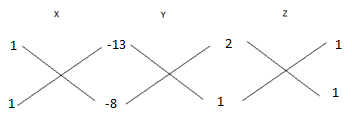
Here z=1
\[\begin{align}
& x=\dfrac{{{b}_{1}}{{c}_{2}}-{{b}_{2}}{{c}_{1}}}{{{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}}}=\dfrac{1\times (-8)-1\times (-13)}{2\times 1-1\times 1}=\dfrac{-8+13}{2-1}=\dfrac{5}{1}=5 \\
& y=\dfrac{{{c}_{1}}{{a}_{2}}-{{c}_{2}}{{a}_{1}}}{{{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}}}=\dfrac{(-13\times 1)-(-8\times 2)}{(2\times 1)-(1\times 1)}=\dfrac{-13+16}{2-1}=3 \\
\end{align}\]
Thus we got x = 5 and y = 3, i.e. the value we got by cross multiplication is (5, 3).
Option A is the correct answer.
Note: If the value of x or y is zero, that is \[\left( {{b}_{1}}{{c}_{2}}-{{b}_{2}}{{c}_{1}} \right)=0\] or \[\left( {{c}_{1}}{{a}_{2}}-{{c}_{2}}{{a}_{1}} \right)=0\], it is not proper way to express in the formula for cross multiplication, because the denominator of a fraction can never be zero. For two simultaneous equations, cross multiplication is an important concept.
Complete step-by-step answer:
We have been given two equations \[2x+y=13.....(1)\]
\[x+y=8....(2)\]
Now let us look into the formula for cross multiplication and its use in solving two simultaneous equations can be presented as,
\[\begin{align}
& {{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}=0......(3) \\
& {{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}=0.....(4) \\
\end{align}\]
Thus we can draw it as,

Here z=1
Thus from this we can write as,
\[\dfrac{x}{{{b}_{1}}{{c}_{2}}-{{b}_{2}}{{c}_{1}}}=\dfrac{y}{{{c}_{1}}{{a}_{2}}-{{c}_{2}}{{a}_{1}}}=\dfrac{1}{{{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}}}\]
From this we can write,
\[\begin{align}
& \dfrac{x}{{{b}_{1}}{{c}_{2}}-{{b}_{2}}{{c}_{1}}}=\dfrac{1}{{{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}}} \\
& \Rightarrow x=\dfrac{{{b}_{1}}{{c}_{2}}-{{b}_{2}}{{c}_{1}}}{{{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}}}.....(5) \\
\end{align}\]
\[\begin{align}
& \dfrac{y}{{{c}_{1}}{{a}_{2}}-{{c}_{2}}{{a}_{1}}}=\dfrac{1}{{{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}}} \\
& \therefore y=\dfrac{{{c}_{1}}{{a}_{2}}-{{c}_{2}}{{a}_{1}}}{{{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}}}....(6) \\
\end{align}\]
Thus from equation (1) , \[2x+y-13=0\], compare it with equation (3).
\[{{a}_{1}}=2,{{b}_{1}}=1,{{c}_{1}}=-13\]
Now from equation (2), \[x+y=8\], compare it with equation (4).
\[{{a}_{2}}=1,{{b}_{2}}=1,{{c}_{2}}=-8\]
Now apply these values in equation (5) and (6).
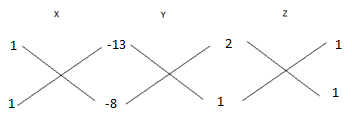
Here z=1
\[\begin{align}
& x=\dfrac{{{b}_{1}}{{c}_{2}}-{{b}_{2}}{{c}_{1}}}{{{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}}}=\dfrac{1\times (-8)-1\times (-13)}{2\times 1-1\times 1}=\dfrac{-8+13}{2-1}=\dfrac{5}{1}=5 \\
& y=\dfrac{{{c}_{1}}{{a}_{2}}-{{c}_{2}}{{a}_{1}}}{{{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}}}=\dfrac{(-13\times 1)-(-8\times 2)}{(2\times 1)-(1\times 1)}=\dfrac{-13+16}{2-1}=3 \\
\end{align}\]
Thus we got x = 5 and y = 3, i.e. the value we got by cross multiplication is (5, 3).
Option A is the correct answer.
Note: If the value of x or y is zero, that is \[\left( {{b}_{1}}{{c}_{2}}-{{b}_{2}}{{c}_{1}} \right)=0\] or \[\left( {{c}_{1}}{{a}_{2}}-{{c}_{2}}{{a}_{1}} \right)=0\], it is not proper way to express in the formula for cross multiplication, because the denominator of a fraction can never be zero. For two simultaneous equations, cross multiplication is an important concept.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




