Question

Find the value of x and y in the following figure.

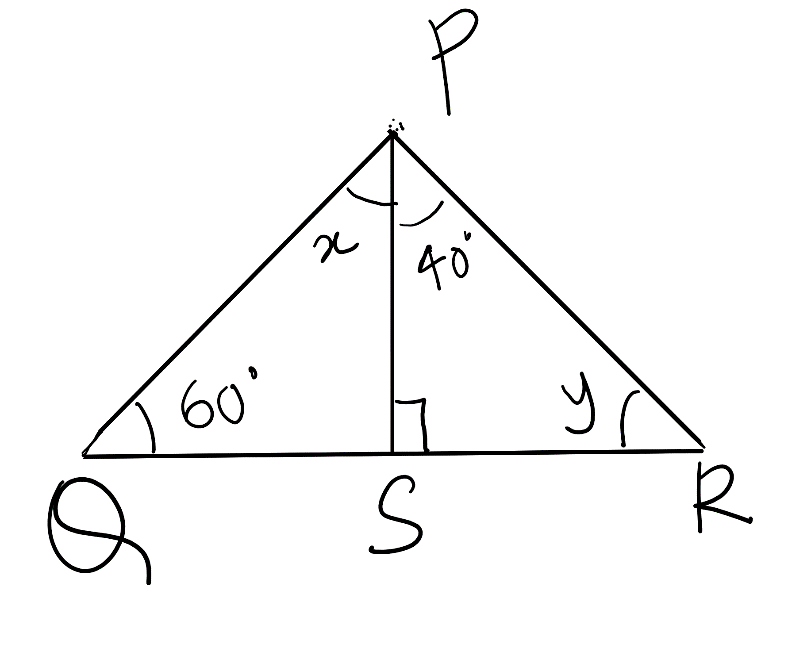
Answer 1

Hint: We will use the angle sum property of triangles to solve this question. It is stated as “The Angle sum property of the triangle states that the sum of interior angles of a triangle is 180°”.

Complete step-by-step solution -

We are given the figure as,

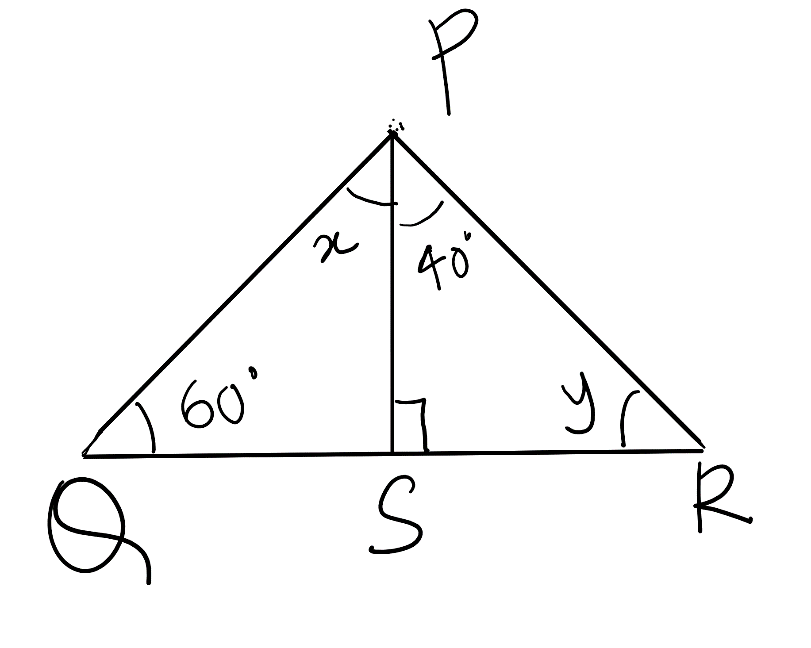
We have to find the value of x and y.
We will use the angle sum property of the triangle to solve this question.
The Angle sum property of a triangle states that the sum of interior angles of a triangle is 180°.
Observing the given triangle PQR, we see that there are 2 triangles PSR and triangle PSQ.
Given that the angle PSR is 90 degrees and because QSR is the line, therefore, the angle QSR would be 180.
Then we get the value of angle PSQ = 180-90 = 90.
Hence, we obtained the angle PSQ and PSR are both $90^0$.
Now we will use angle sum property of triangle to solve further which is stated as,
The Angle sum property of a triangle states that the sum of interior angles of a triangle is 180°.
Consider \[\Delta PSR\],
Applying angle sum property of triangle, we get,
\[\angle P+\angle S+\angle R={{180}^{0}}\]
Substituting the value of angle P as $40^0$, angle S as $90^0$ and angle R as y we get,
\[\begin{align}
  & \angle P+\angle S+\angle R={{180}^{0}} \\
 & \Rightarrow {{40}^{0}}+{{90}^{0}}+y={{180}^{0}} \\
 & \Rightarrow {{130}^{0}}+y={{180}^{0}} \\
 & \Rightarrow y={{180}^{0}}-{{130}^{0}} \\
 & \Rightarrow y={{50}^{0}} \\
\end{align}\]
Therefore, we get the value of y as y = $50^0$.
Similarly, applying the angle sum property of triangle in \[\Delta PSQ\], we get,
 \[\angle P+\angle S+\angle Q={{180}^{0}}\]
Substituting the value of angle Q as $60^0$, angle P as x and angle S as $90^0$, we get,
\[\begin{align}
  & \angle P+\angle S+\angle Q={{180}^{0}} \\
 & \Rightarrow {{60}^{0}}+{{90}^{0}}+x={{180}^{0}} \\
 & \Rightarrow {{150}^{0}}+x={{180}^{0}} \\
 & \Rightarrow x={{180}^{0}}-{{150}^{0}} \\
 & \Rightarrow x={{30}^{0}} \\
\end{align}\]
Therefore, we got the value of x as x = $30^0$.
So, we get the value of x = $30^0$ and y = $50^0$.

Note: The possibility of error in this type of question can be at the point where you can assume that the angle PSQ is 90 degrees which is not wrong in this question but can be wrong in other questions, because we need to find out the value of angle first before using it.