Question

Find the value of $\underset{x\to 0}{\mathop{\lim }}\,{{\left( \sin x \right)}^{2\tan x}}$.
A. 2 B. 1 C. 0 D. doesn’t exist

Answer 1

Hint: We try to put the points on the graph to find out the limit of the function. From the graph, we find out if both sides limit for the function exists or not. If they exist and are equal then we place the value as a solution otherwise limit doesn’t exist.

Complete step by step answer:
The given is $y=\underset{x\to 0}{\mathop{\lim }}\,{{\left( \sin x \right)}^{2\tan x}}$.
We draw the graph of the function and get

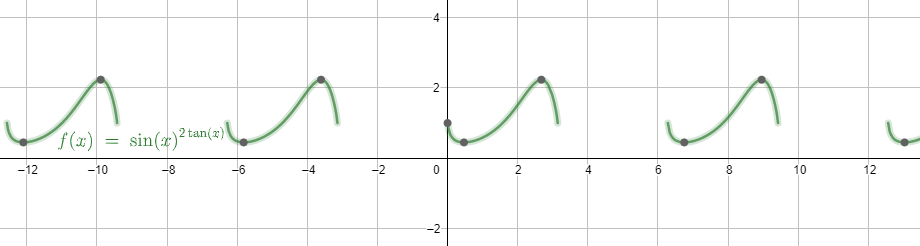
From the figure, we can see the graph is discontinuous at x = 0.
Although the right-hand side limit exists at point $\left( 0,1 \right)$, the left-hand side doesn’t. so, the limit doesn’t exist altogether.
We now find the right-hand side limit.
We take logarithm both side of the function $y=\underset{x\to 0}{\mathop{\lim }}\,{{\left( \sin x \right)}^{2\tan x}}$.
So, \[\log y=\log \left( \underset{x\to 0}{\mathop{\lim }}\,{{\left( \sin x \right)}^{2\tan x}} \right)=\underset{x\to 0}{\mathop{\lim }}\,\log \left[ {{\left( \sin x \right)}^{2\tan x}} \right]=\underset{x\to 0}{\mathop{\lim }}\,\left[ 2\tan x\log \left( \sin x \right) \right]\]
Now, we apply the theorem of limit to break two multiplication.
We know $\underset{x\to a}{\mathop{\lim }}\,\left[ \left( f\left( x \right) \right)\left( g\left( x \right) \right) \right]=\underset{x\to a}{\mathop{\lim }}\,\left[ \left( f\left( x \right) \right) \right]\times \underset{x\to a}{\mathop{\lim }}\,\left[ \left( g\left( x \right) \right) \right]$
We get \[\underset{x\to 0}{\mathop{\lim }}\,\left[ 2\tan x\log \left( \sin x \right) \right]=\underset{x\to 0}{\mathop{\lim }}\,\left[ 2\tan x \right]\times \underset{x\to 0}{\mathop{\lim }}\,\left[ \log \left( \sin x \right) \right]\].
Now we find the value of the limit as
\[\begin{align}
  & \log y=\underset{x\to 0}{\mathop{\lim }}\,\left[ 2\tan x \right]\times \underset{x\to 0}{\mathop{\lim }}\,\left[ \log \left( \sin x \right) \right] \\
 & \Rightarrow \log y=0\times \underset{x\to 0}{\mathop{\lim }}\,\left[ \log \left( \sin x \right) \right]=0 \\
 & \Rightarrow y={{e}^{0}}=1 \\
\end{align}\]
So, the value of the limit(right-hand) is 1. But the left-hand side doesn’t exist as for \[\log \left( \sin x \right)\] the value of $\sin x$ is negative when $x\to {{0}^{-}}$. So, in that case we get logarithm of negative value which is not possible.
So, the correct option is (D).
Note:
 Although we find the graph value as a limit non-existent, we still need to show the right-hand limit. In case of left-hand limit, although the \[\underset{x\to 0}{\mathop{\lim }}\,\left[ 2\tan x \right]\] omit the all possible options for rest, the rest still has to be viable for existence. That’s why that limit can’t exist.