Question

Find the value of $\theta $ in the given trigonometric equation $\dfrac{\cos \theta }{1-\sin \theta }+\dfrac{\cos \theta }{1+\sin \theta }=4$ such that $\theta \in \left[ 0,2\pi \right]$

Answer 1

Hint: Take LCM of denominators and simplify the given relation using the identity ${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1,{{\sin }^{2}}\theta =1-{{\cos }^{2}}\theta $ . Find the values of $\theta $ with the help of a graph of $y=\cos \theta $ and verify it with the domain of the given relation. Use relation ${{a}^{2}}-{{b}^{2}}=\left( a-b \right)\left( a+b \right)$ whenever necessary.

Complete step-by-step answer:
Here, we have
$\dfrac{\cos \theta }{1-\sin \theta }+\dfrac{\cos \theta }{1+\sin \theta }=4...............\left( i \right)$
Such that $\theta \in \left[ 0,2\pi \right]$ and we need to determine values of $\theta $ by solving the above equation. So, we can take $\cos \theta $ as common in LHS of equation (i) so, we get
$\cos \theta \left[ \dfrac{1}{1-\sin \theta }+\dfrac{1}{1+\sin \theta } \right]=4$
Now, take the LCM of the denominator of the fractions inside the bracket. Hence we get,
\[\begin{align}
  & \cos \theta \left[ \dfrac{\left( 1+\sin \theta \right)+\left( 1-\sin \theta \right)}{\left( 1-\sin \theta \right)\left( 1+\sin \theta \right)} \right]=4 \\
 & \cos \theta \left[ \dfrac{1+\sin \theta +1-\sin \theta }{\left( 1-\sin \theta \right)\left( 1+\sin \theta \right)} \right]=4 \\
 & \cos \theta \left[ \dfrac{2}{\left( 1-\sin \theta \right)\left( 1+\sin \theta \right)} \right]=4 \\
\end{align}\]
Now, we can use an algebraic identity to solve \[\left( 1-\sin \theta \right)\left( 1+\sin \theta \right)\], which is given as
$\left( a-b \right)\left( a+b \right)={{a}^{2}}-{{b}^{2}}$
So, we get
$\begin{align}
  & \cos \theta \left[ \dfrac{2}{{{1}^{2}}-{{\sin \theta }^{2}}} \right]=4 \\
 & \dfrac{2\cos \theta }{1-{{\sin }^{2}}\theta }=4 \\
 & \dfrac{\cos \theta }{1-{{\sin \theta }^{2}}}=2 \\
\end{align}$
Now, on cross multiplication the above equation, we get
$\cos \theta =2\left( 1-{{\sin }^{2}}\theta \right)............\left( ii \right)$
Now, we can get above equation only in terms of $\cos \theta $ by replacing ${{\sin }^{2}}\theta $ to $1-{{\cos }^{2}}\theta $ by the trigonometric identity, given as
$\begin{align}
  & {{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1 \\
 & {{\sin }^{2}}\theta =1-{{\cos }^{2}}\theta \\
\end{align}$
Hence, we can rewrite equation (ii) as
$\begin{align}
  & \cos \theta =2\left( 1-\left( 1-{{\cos }^{2}}\theta \right) \right) \\
 & \cos \theta =2\left( 1-1+{{\cos }^{2}}\theta \right) \\
 & \cos \theta =2{{\cos }^{2}}\theta \\
 & 2{{\cos }^{2}}\theta -\cos \theta =0 \\
\end{align}$
Now, taking $\cos \theta $ as common from the above equation in LHS, we get
$\cos \theta \left( 2\cos \theta -1 \right)=0..............\left( iii \right)$
As we know multiplication of two terms will be ‘0’ if one or both of them is 0. Hence, we get from equation (iii) as
\[\begin{align}
  & \cos \theta =0,2\cos \theta -1=0 \\
 & \cos \theta =0,\cos \theta =\dfrac{1}{2} \\
\end{align}\]
Now it is given that $\theta \in \left[ 0,2\pi \right]$ , which means we need to determine values of $\theta $ lying in $\left[ 0,2\pi \right]$ only for the equations $\cos \theta =0,\cos \theta =\dfrac{1}{2}$ . So, let us draw a graph of $\cos \theta $ from $\left[ 0,2\pi \right]$ which will give us all the values for the above equations. We know the graph of $y=\cos \theta $ can be given as

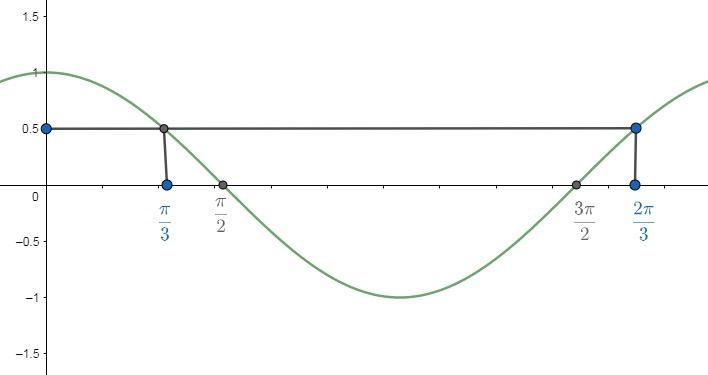
Now, we can observe that $\cos \theta $ will give value as ‘0’ at the angles $\dfrac{\pi }{2},\dfrac{3\pi }{2}$ . Hence, solutions for $\cos \theta =0$ are $\dfrac{\pi }{2},\dfrac{3\pi }{2}$ . Similarly solution of equation $\cos \theta =\dfrac{1}{2}$ will lie in \[\left( 0,\dfrac{\pi }{2} \right),\left( \dfrac{3\pi }{2},2\pi \right)\] and can be given as $\dfrac{\pi }{3}$ in $\left( 0,\dfrac{\pi }{2} \right)$ and $2\pi -\dfrac{\pi }{3}=\dfrac{5\pi }{3}$ in $\left( \dfrac{3\pi }{2},2\pi \right)$ .
Now, we can observe the given expression and we cannot put $\theta =\dfrac{\pi }{2},\dfrac{3\pi }{2}$ to the expression as $\sin \dfrac{\pi }{2}=1,\sin \dfrac{3\pi }{2}=-1.$ So, we get infinite for $\dfrac{\cos \theta }{1-\sin \theta },\dfrac{\cos \theta }{1+\sin \theta }$ if $\theta =\dfrac{\pi }{2},\dfrac{3\pi }{2}.$ So, these values of $\theta $ are not possible. Hence, we can ignore these values.