Question

Find the value of the expression $\cos ec\left( -{{1200}^{\circ }} \right)$

Answer 1

Hint: Apply the trigonometric identity, given as

$\cos ec\left( -x \right)=-\cos ecx$

Write the given angle in the bracket of trigonometric function as sum of the angle, which is multiple of ${{180}^{\circ }}$ or $\pi $ i.e convert the given angle of $n\pi \pm \theta $ type. Observe the quadrant in which the angle is lying and the sign of the function in that quadrant as well. Do not change the trigonometric function while conversion, as angle is in multiple of $\pi \left( n\pi \right)$

Use: $\cos ec\dfrac{\pi }{3}=\dfrac{2}{\sqrt{3}}$

Complete step-by-step answer:

Suppose the given term/expression in the problem as ‘P’. So, we get $P=\cos ec\left( -{{1200}^{\circ }} \right)$

Now, as the angle inside the expression is negative. So, we need to use the following trigonometric identity of cosec functions, given as

$\cos ec\left( -\theta \right)=-\cos ec\theta .............\left( ii \right)$

So, with the help of equation(ii), we can rewrite the given expression in the problem i.e. equation(ii), as

$\begin{align}

  & P=\cos ec\left( -1200 \right)=-\cos ec1200 \\

 & \Rightarrow P=-\cos ec\left( {{1200}^{\circ }} \right)...............\left( iii \right) \\

\end{align}$

Now, we can observe that the angle involved in the above expression is not lying in ${{0}^{\circ }}$ to ${{90}^{\circ }}$ i.e. not acute angle and we have known values of trigonometric functions only in ${{0}^{\circ }}$ to ${{90}^{\circ }}$ . It means we have to convert the given angle to acute angle form with the help of some trigonometric identities.

Hence, let us divide the given expression by ${{180}^{\circ }}$ , so that we can write the given angle in form of sum of angle which is multiple of ${{180}^{\circ }}$ in following way:

$1200=180\times 7-60$

Now, as we know the radian representation of ${{180}^{\circ }}$ is given as

$\pi $ radian = ${{180}^{\circ }}.............\left( iv \right)$

And with the help of above relation, we can rewrite the angle ${{60}^{\circ }}$ in radian form as well, given as

${{60}^{\circ }}=\dfrac{\pi }{3}.........\left( v \right)$

Now, we can put angle ${{1200}^{\circ }}$ as $7\pi -\dfrac{\pi }{3}$ from the above expressions. So, we can write equation(iii) as

$P=-\cos ec\left( 7\pi -\dfrac{\pi }{3} \right).............\left( vi \right)$

Now, as we know the quadrant angles are defined as

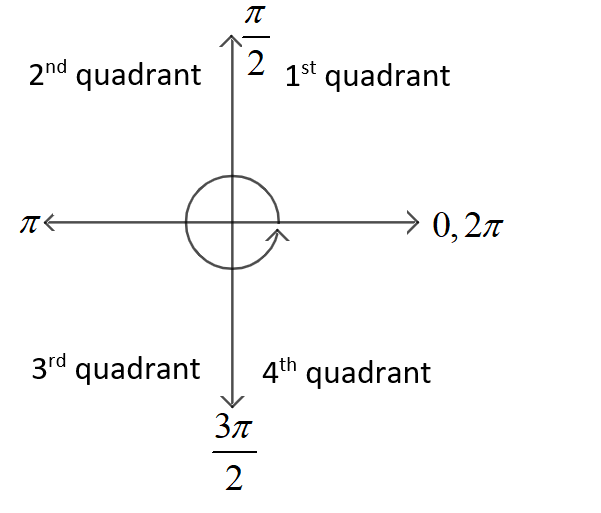
Now, we can apply the trigonometric rules for conversion of trigonometric expressions by changing its angle.

We can observe the angle in equation(vi) and hence, get that the angle $\left( 7\pi -\dfrac{\pi }{3} \right)$ will lie definitely in 2nd quadrant as $7\pi $ will lie at same position where $\pi $ is lying (after first rotation to ${{360}^{\circ }}$ or $2\pi $ ).

So, we know that cosec function is positive in 2nd quadrant and we know very well that the angle involved in the equation(iv) is $7\pi $ i.e. multiple of $'\pi '$ so the trigonometric function will not change while changing the angle as per the trigonometric rules for conversion.

So, we can write trigonometric identity as

\[\begin{align}

  & \cos ec\left( \pi -\theta \right)=\cos ec\theta \\

 & \cos ec\left( 3\pi -\theta \right)=\cos ec\theta \\

 & \cos ec\left( 5\pi -\theta \right)=\cos ec\theta \\

 & .\text{ }\text{. }\text{. }\text{. }\text{.} \\

 & .\text{ }\text{. }\text{. }\text{. }\text{.} \\

 & .\text{ }\text{. }\text{. }\text{. }\text{.} \\

 & .\text{ }\text{. }\text{. }\text{. }\text{.} \\

 & \cos ec\left( n\pi -\theta \right)=\cos ec\theta \\

\end{align}\]

$P=-\cos ec\left( 7\pi -\dfrac{\pi }{3} \right)=-\cos ec\dfrac{\pi }{3}$

Now, we know the angle of $\cos ec\dfrac{\pi }{3}$ is given as $\dfrac{\sqrt{2}}{3}$ . Hence we get the value of P as

$\begin{align}

  & P=-\cos ec\left( \dfrac{\pi }{3} \right)=\dfrac{-2}{\sqrt{3}} \\

 & P=\dfrac{-2}{\sqrt{3}} \\

\end{align}$

So, the value of expression given in the problem is $\dfrac{-2}{\sqrt{3}}$ . So, we get

$\cos ec\left( -{{1200}^{\circ }} \right)=\dfrac{-2}{\sqrt{3}}$

Hence, $\dfrac{-2}{\sqrt{3}}$ is the answer of the problem.

Note: One may not be able to get the exact value of $\cos ec\left( -{{1200}^{\circ }} \right)$ directly without using the identity $\cos ec\left( -\theta \right)=-\cos ec\theta $ . So, apply the relation to get a familiar relation and then proceed further, which is the key point of the problem as well.
We need to know two important rules involved for conversion of trigonometric functions with respect to the angles.
(i) Take care of the sign with the help of the given trigonometric function and the quadrant in which the angle is lying. This rule can be given ass
(ii) If the angle involved inside trigonometric function is multiply of $\dfrac{\pi }{2}$ (not multiple of $\pi $ ) i.e. $\dfrac{n\pi }{2}\pm \theta $ type, where n is an odd integer, then we need to convert the
$\begin{align}
  & \sin \rightleftarrows \cos \\
 & \tan \rightleftarrows \cot \\
 & \sec \rightleftarrows \cos ec \\
\end{align}$
and if the angle involved in the sum is multiple of $\pi $ i.e. $n\pi \pm \theta $ type, then the trigonometric function will remain the same. Use the above two rules for conversion of any trigonometric function by changing their angles.