Question

Find the value of $\tan \left( 90{}^\circ -\theta \right)$
[a] $\sin \theta $
[b] $\cos \theta $
[c] $\sin \theta +\cos \theta $
[d] $\cot \theta $

Answer 1

Hint: In a right triangle, ABC is right-angled at A if $\angle C=\theta $ then $\angle B=90{}^\circ -\theta $. Use the fact that \[\sin \theta =\dfrac{\text{Perpendicular}}{\text{Hypotenuse}}\] and \[\cos \theta =\dfrac{\text{Base}}{\text{Hypotenuse}}\] and $\tan \theta =\dfrac{\text{Perpendicular}}{\text{Base}}$

Complete step-by-step answer:

Trigonometric ratios:
There are six trigonometric ratios defined on an angle of a right-angled triangle, viz sine, cosine, tangent, cotangent, secant and cosecant.
The sine of an angle is defined as the ratio of the opposite side to the hypotenuse.
The cosine of an angle is defined as the ratio of the adjacent side to the hypotenuse.
The tangent of an angle is defined as the ratio of the opposite side to the adjacent side.
The cotangent of an angle is defined as the ratio of the adjacent side to the opposite side.
The secant of an angle is defined as the ratio of the hypotenuse to the adjacent side.
The cosecant of an angle is defined as the ratio of the hypotenuse to the adjacent side.
Observe that sine and cosecant are multiplicative inverses of each other, cosine and secant are multiplicative inverses of each other, and tangent and cotangent are multiplicative inverses of each other.

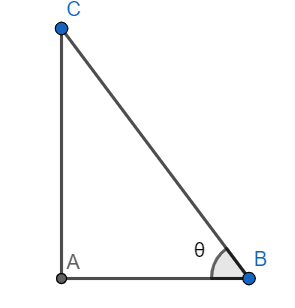
In the given figure ABC is a right-angled triangle right-angled at A
$\angle B=\theta $
Now we know that, from the property of a triangle, Sum of the angles of a triangle is
 $\angle A+\angle B+\angle C=180$
Substituting the value of $\angle A$ and $\angle B$ we get
\[\begin{align}
  & 90{}^\circ +\theta +\angle C=180{}^\circ \\
 & \Rightarrow \angle C=180{}^\circ -90{}^\circ -\theta \\
 & \Rightarrow \angle C=90{}^\circ -\theta \\
\end{align}\]
Now $\tan C=\dfrac{AB}{AC}$ and $\tan B=\dfrac{AC}{AB}$
Hence $\tan C\tan B=\dfrac{AB}{AC}\times \dfrac{AC}{AB}=1$
Hence $\tan C=\dfrac{1}{\tan B}=\cot B$
Put the value of C and B, we get
$\tan \left( 90{}^\circ -\theta \right)=\cot \theta $
Hence option [d] is correct.
Note:
[1] sin(90-x) = cosx
[2] cos(90-x) = sinx
[3] tan(90-x) = cotx
[4] cot(90-x) = tanx
[5] sec(90-x) = cosecx
[6] cosec(90-x) = secx