Question

Find the value of $\tan 5x$ , if $\cos 9x=\sin x\text{ and 9}x<90{}^\circ $ .
(a) $\dfrac{1}{\sqrt{2}}$
(b) $\dfrac{1}{\sqrt{3}}$
(c) 1
(d) $\dfrac{1}{2}$

Answer 1

Hint: Use the property that $\sin \left( 90{}^\circ -A \right)=\cos A$ to simplify the equation given in the question. Now you need to ensure that 9x and x both lie in the first quadrant and using this you need to draw a relation between 9x and x to get the value of x. Once you get x, it is easy to find the value of tan5x using the trigonometric table.

Complete step-by-step answer:
Before moving to the solution, let us discuss the periodicity of sine and cosine function, which we would be using in the solution. All the trigonometric ratios, including sine and cosine, are periodic functions. We can better understand this using the graph of sine and cosine.
First, let us start with the graph of sinx.

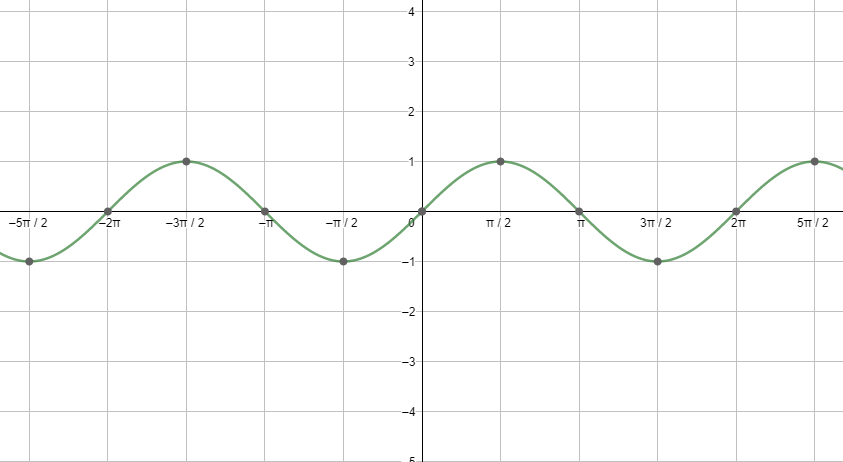
Next, let us see the graph of cosx.

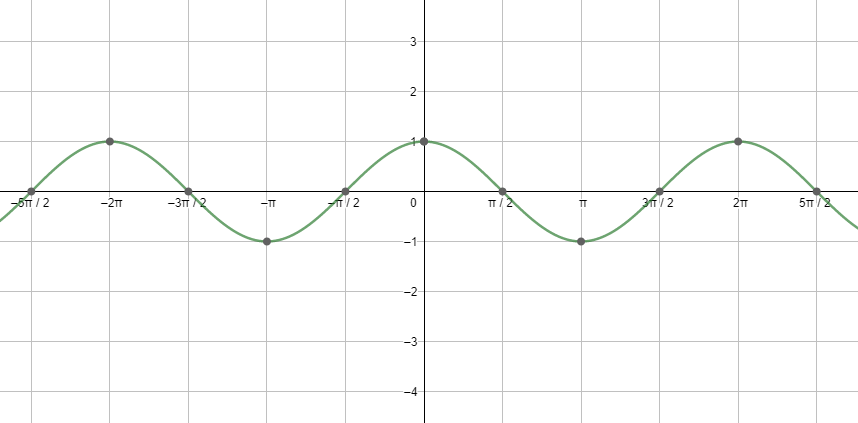
Looking at both the graphs, we can say that the graphs are repeating after a fixed period i.e. $2{{\pi }^{c}}$ . So, we can say that the fundamental period of the cosine function and the sine function is $2{{\pi }^{c}}=360{}^\circ $
Now to start with the solution to the above question, we will try to simplify the equation given in the question using the property that $\sin \left( 90{}^\circ -A \right)=\cos A$ .
$\cos 9x=\sin x$
$\Rightarrow \cos 9x=\cos \left( 90{}^\circ -x \right)$
Now it is given that $9x<90{}^\circ $ , which implies that 9x lies in the first quadrant. We can also use this to say that x is less than $10{}^\circ $ , hence $\left( 90{}^\circ -x \right)$ also lies in the first quadrant.
Therefore, using the above equation, we can say that:
$9x=90{}^\circ -x$
$\Rightarrow 10x=90{}^\circ $
$\Rightarrow x=9{}^\circ $
Now we will move on to finding the value of tan5x.
$\tan 5x=\tan 5\times 9{}^\circ =\tan 45{}^\circ $
We know that the value of $\tan 45{}^\circ =1$ . So, we can conclude that the value of tan5x is equal to 1. Hence, the answer to the above question is option (c).

Note: Be careful about the calculation and the signs of the formulas you use as the signs in the formulas are very confusing and are very important for solving the problems. Also, it would help if you remember the properties related to complementary angles and trigonometric ratios.
Remember that cosx=cosy doesn’t mean that x=y, the result is only true if some condition bounds x and y to be equal, as we saw in the above question the restriction that both are in the x and 9x are in the first quadrant is bounding them to be equal. In general, cosx=cosy implies $x=2n\pi \pm y$ .