Question

Find the value of $\sin \left( \pi +x \right)\sin \left( \pi -x \right)\cos e{{c}^{2}}x$.

Answer 1

Hint: Start with the simplification of the expression given in the question. First, convert all the terms as a function of sine and cosine, followed by the applying of the formula: $\sin \left( \pi +x \right)=-\sin x\text{ and }\sin \left( \pi -x \right)=\sin x$.

Complete step-by-step answer:

Before moving to the solution, let us discuss the periodicity of sine and cosine function, and their relation with cosine and secant functions, which we would be using in the solution.
First, let us start with the graph of sinx and cosecx.

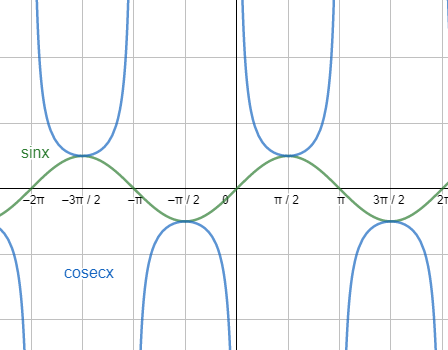
Next, let us see the graph of cosx and secx.

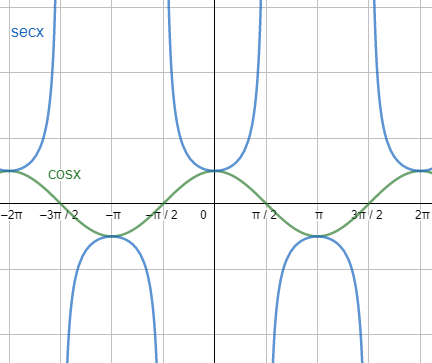
From the above graphs, we can say that the reciprocal of sinx is the value of cosecx, and the reciprocal of cosx is the value of secx.

Now to start with the solution, let us use the property that $\cos ecX=\dfrac{1}{\sin X}$ .

$\sin \left( \pi +x \right)\sin \left( \pi -x \right)\cos e{{c}^{2}}x$

$=\sin \left( \pi +x \right)\sin \left( \pi -x \right)\times \dfrac{1}{{{\sin }^{2}}x}$

From the graph of sinx, we can see that $\sin \left( \pi +x \right)=-\sin x\text{ and }\sin \left( \pi -x \right)=\sin x$. So, our expression becomes:

$=-{{\sin }^{2}}x\times \dfrac{1}{{{\sin }^{2}}x}$

$=-1$

Therefore, the value of the expression $\sin \left( \pi +x \right)\sin \left( \pi -x \right)\cos e{{c}^{2}}x$ is equal to -1.

Note: It is useful to remember the graph of the trigonometric ratios along with the signs of their values in different quadrants. For example: sine is always positive in the first and the second quadrant while negative in the other two. Also, remember the relation of different trigonometric ratios with each other.