Question

Find the value of $\sin \left( 2{{\sin }^{-1}}\dfrac{3}{5} \right)$ .

Answer 1

Hint: In a right-angled triangle with length of the side opposite to angle θ as perpendicular (P), base (B) and hypotenuse (H):
 $\sin \theta =\dfrac{P}{H},\cos \theta =\dfrac{B}{H},\tan \theta =\dfrac{P}{B}$
${{P}^{2}}+{{B}^{2}}={{H}^{2}}$ (Pythagoras Theorem)
sin 2θ = 2 sin θ cos θ.
If sin θ = x, then we say ${{\sin }^{-1}}x=\theta $ .
$\sin ({{\sin }^{-1}}x)=x$ .

Complete step-by-step answer:
Let's say that ${{\sin }^{-1}}\dfrac{3}{5}=\theta $ .
∴ By the definition of inverse trigonometric functions, $\sin \theta =\dfrac{3}{5}$ .
And, by the definition of trigonometric ratios, $\sin \theta =\dfrac{P}{H}$ and $\cos \theta =\dfrac{B}{H}$ .
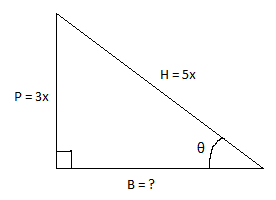
∴ P = 3x and H = 5x.
It can be represented using a right-angled triangle as follows:

Using the Pythagoras' Theorem:
 $B=\sqrt{{{H}^{2}}-{{P}^{2}}}=\sqrt{{{(5x)}^{2}}-{{(3x)}^{2}}}=\sqrt{25{{x}^{2}}-9{{x}^{2}}}=\sqrt{16{{x}^{2}}}=4x$ .
And thus, $\cos \theta =\dfrac{B}{H}=\dfrac{4x}{5x}=\dfrac{4}{5}$ .
Now, using the identity sin 2θ = 2 sin θ cos θ, and substituting the values of $\sin \theta =\dfrac{3}{5}$ and $\cos \theta =\dfrac{4}{5}$ from above, we will get:
 $\sin \left( 2{{\sin }^{-1}}\dfrac{3}{5} \right)=2\left( \dfrac{3}{5} \right)\left( \dfrac{4}{5} \right)$
On multiplying the terms on the Right-Hand Side of the equation together, we get:
⇒ $\sin \left( 2{{\sin }^{-1}}\dfrac{3}{5} \right)=\dfrac{24}{25}$ .
Hence, the value of $\sin \left( 2{{\sin }^{-1}}\dfrac{3}{5} \right)$ is $\dfrac{24}{25}$

Note: The inverse trigonometric functions, ${{\sin }^{-1}},{{\cos }^{-1}},{{\tan }^{-1}}$ ... etc. represent the value of an angle.
The inverse trigonometric functions, ${{\sin }^{-1}},{{\cos }^{-1}},{{\tan }^{-1}}$ ... etc. are also written as arcsin, arccos, arctan ... etc.
If one trigonometric ratio is known, we can use Pythagoras' Theorem and calculate the values of all other trigonometric ratios.
 ${{\sin }^{-1}}\dfrac{3}{5}=36.87{}^\circ $ .