Question

Find the value of $\sin {37^o},\sin {53^o},\tan {37^o},\tan {53^o}$ in terms of fraction.

Answer 1

Hint: In this question, we have to write the given trigonometric function in terms of fraction.
We know, that in a right- angled triangle, there are three sides, perpendicular, base and the hypotenuse.
And, $\sin \theta = \dfrac{P}{H}$ , where, $P$ is the length of perpendicular and $H$ is referred to as the length of hypotenuse, whereas, $\tan \theta = \dfrac{P}{B}$ , where, $P$ is the length of perpendicular and $B$ is the length of base of the triangle.

Complete answer:
Given trigonometric functions $\sin {37^o},\sin {53^o},\tan {37^o},\tan {53^o}$ .
To write these trigonometric functions in terms of fraction.
Consider a right- angled triangle, $\vartriangle ABC$ , with $\angle ACB = {37^o}$ and $\angle ABC = {90^o}$ .

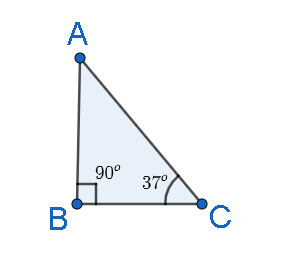
Then, we have, using angle sum property of a triangle, that, $\angle ABC + \angle BAC + \angle ACB = {180^o}$ , i.e., ${37^o} + {90^o} + \angle BAC = {180^o}$ . On solving, we get, $\angle BAC = {180^o} - {127^o}$ i.e., $\angle BAC = {53^o}$ .
Now, let length of side $AB$ is $3units$ and length of side $BC$ is $4units$ , then, by Pythagoras theorem, we have, $A{B^2} + B{C^2} = A{C^2}$ , putting values, we get, ${3^2} + {4^2} = 9 + 16 = 25$ , hence, $AC = 5units$ .
Now, we know, $\sin \theta = \dfrac{P}{H}$ , and for angle $\theta = {37^o}$ , $P = 3$ and $H = 5$ . So, $\sin {37^o} = \dfrac{3}{5}$ .
Similarly, for angle $\theta = {53^o}$ , $P = 4$ and $H = 5$ . So, $\sin {53^o} = \dfrac{4}{5}$ .
Now, for angle $\theta = {37^o}$ , $P = 3$ and $B = 4$ . So, $\tan {37^o} = \dfrac{3}{4}$ .
Similarly, for angle $\theta = {53^o}$ , $P = 4$ and $B = 3$ . So, \[\tan {53^o} = \dfrac{4}{3}\]

Note:
It is not necessary to choose the lengths of sides of the triangle to be $3units$ or $4units$ . We can choose the length of sides of the right- angled triangle by our choices.
If ${x^2} = {a^2}$ , then, taking square root on both sides, we get, $x = \pm a$ , but in this question, we are talking about length of sides and length can never be negative. Hence, we have taken only the positive one.
For any angle, say $\theta $ , the sides opposite to this angle will be the perpendicular side, whereas, the third side except for the hypotenuse, will be the base of the triangle.